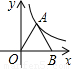
题目内容
 如图,正△AOB的顶点A在反比例函数y=
如图,正△AOB的顶点A在反比例函数y=
| ||
| x |
(2,0)
(2,0)
.分析:过点A作AC⊥OB于点C,设A(x,
),则OC=x,OB=2x,再根据锐角三角函数的定义求出x的值即可.
| ||
| x |
解答: 解:过点A作AC⊥OB于点C,设A(x,
解:过点A作AC⊥OB于点C,设A(x,
),则OC=x,OB=2x,
∵△AOB是等边三角形,
∴∠AOC=60°,
∴
=tan60°,
=
,解得x=±1,
∵点C在x轴的正半轴上,
∴x=1,
∴OB=2x=2,即B(2,0).
故答案为:(2,0).
 解:过点A作AC⊥OB于点C,设A(x,
解:过点A作AC⊥OB于点C,设A(x,
| ||
| x |
∵△AOB是等边三角形,
∴∠AOC=60°,
∴
| AC |
| OC |
| ||||
| x |
| 3 |
∵点C在x轴的正半轴上,
∴x=1,
∴OB=2x=2,即B(2,0).
故答案为:(2,0).
点评:本题考查的是反比例函数图象上点的坐标特点及等边三角形的性质,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
 如图,正△AOB的顶点A在反比例函数y=
如图,正△AOB的顶点A在反比例函数y=
| ||
| x |
| A、(2,0) | ||||
B、(
| ||||
C、(2
| ||||
D、(
|
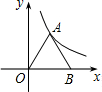 如图,正△AOB的顶点A在反比例函数y=
如图,正△AOB的顶点A在反比例函数y=
| ||
| x |
A、(1,
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
 如图,正△AOB的顶点A在反比例函数y=
如图,正△AOB的顶点A在反比例函数y= (x>0)的图象上,则正△AOB的面积是 .
(x>0)的图象上,则正△AOB的面积是 .