Question

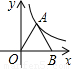
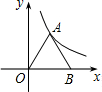如图，正△AOB的顶点A在反比例函数y=

3

x

（x＞0）的图象上，则点A的坐标为（　　）

• A、（1，

  3

  ）
• B、（

  3

  ，1）
• C、（

  1

  2

  ，

  3

  ）
• D、（

  1

  2

  ，

  3

  2

  ）

Answer 1

分析：设正三角形的边长为2x，并用x表示出点A的坐标，代入到反比例函数的解析式中，即可解得x的值，进而可以确定点A的坐标．

解答：解：设正三角形的边长为2x，
∴点A的坐标为：（x，

3

x），
∵点A在反比例函数y=

3

x

（x＞0）的图象上，
∴

3

x=

3

x

，
解得：x=1，
∴点A的坐标为：（1，

3

）．
故选A．

点评：本题考查了反比例函数的应用，解题的关键是利用正三角形的性质求得其高，进而表示出点A的坐标代入函数关系式求解．