题目内容
 如图,梯形ABCD是拦水坝的横断面图,(图中i=1:
如图,梯形ABCD是拦水坝的横断面图,(图中i=1:| 3 |
| 3 |
| 3 |
求(1)∠C的度数;(2)拦水坝的横断面ABCD的面积.
分析:(1)根据坡度即可求得∠C的正切值,根据特殊角的正切值即可求得∠C的度数;
(2)分别求得BC、DE的长,根据梯形面积计算公式即可求梯形ABCD的面积.
(2)分别求得BC、DE的长,根据梯形面积计算公式即可求梯形ABCD的面积.
解答: 解:
解:
(1)∵DE:CE=1:
,
∴tan∠C=
,∵∠C为锐角,∴∠C=30°,
(2)作AF⊥BC,
∵CE=6
,∴DE=
×6
=6,
∴BF=AF•cotB=2
,
∴BC=BF+EF+EC=12
,
∴梯形ABCD的面积为
(BC+AD)DE=
×16
×6=48
.
 解:
解:(1)∵DE:CE=1:
| 3 |
∴tan∠C=
| 1 | ||
|
(2)作AF⊥BC,
∵CE=6
| 3 |
| 1 | ||
|
| 3 |
∴BF=AF•cotB=2
| 3 |
∴BC=BF+EF+EC=12
| 3 |
∴梯形ABCD的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了特殊角的三角函数值,考查了三角函数值在直角三角形中的运用,考查了梯形的面积计算公式,本题中求DE、BC的长是解题的关键.

练习册系列答案
相关题目
 如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
 (2012•凉山州)如图,梯形ABCD是直角梯形.
(2012•凉山州)如图,梯形ABCD是直角梯形.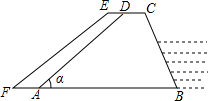 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米. 费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?
费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?