题目内容
已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F、G,连接FG,延长AF、AG,与直线BC相交,易证FG= (AB+AC+BC).
(AB+AC+BC).若:(1)BD、CE分别是△ABC的内角平分线(如图2);
(2)BD为△ABC的内角平分线,CE为△ABC的外角平分线(如图3),
则在图2、图3两种情况下,线段FG与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明.

【答案】分析:(1)都是内角平分线时,可根据等腰三角形三线合一的特点来求解,由于DB平分∠ABC,且AF⊥BD,如果延长AF交BC于K,那么三角形ABK就是个等腰三角形,AF=FK,如果延长AG到H,那么同理可证AG=GH,AC=CH,那么GF就是三角形AHK的中位线,GF就是HK的一半,而HK=BK-BH=BK-(BC-CH),由于BK=AB,CH=AC,那么可得出FG= (AB+AC-BC);
(AB+AC-BC);
(2)证法同(1)先根据题目给出的求法,得出GD是AC的一半,然后按(2)的方法,通过延长AF来得出DF是(BC-AB)的一半,由此可得出FG= (BC+AC-AB).
(BC+AC-AB).
解答: 解:(1)猜想结果:如图结论为FG=
解:(1)猜想结果:如图结论为FG= (AB+AC-BC)
(AB+AC-BC)
证明:分别延长AG、AF交BC于H、K,
在△BAF和△BKF中,
∵ ,
,
∴△BAF≌△BKF(ASA),
∴AF=KF,AB=KB
同理可证,AG=HG,AC=HC
∴FG= HK
HK
又∵HK=BK-BH=AB+AC-BC
∴FG= (AB+AC-BC)
(AB+AC-BC)
(2)图3的结论为FG= (BC+AC-AB).
(BC+AC-AB).
证明:分别延长AG、AF交BC或延长线于H、K
在△BAF和△BKF中,
∵ ,
,
∴△BAF≌△BKF(ASA),
∴AF=KF,AB=KB
同理可证,AG=HG,AC=HC,
∴FG= KH
KH
又∵KH=BC-BK+HC=BC+AC-AB.
∴FG= (BC+AC-AB).
(BC+AC-AB).
点评:本题主要考查了直角三角形的性质,等腰三角形的性质,角平分线的性质以及全等三角形的判定等知识点.
 (AB+AC-BC);
(AB+AC-BC);(2)证法同(1)先根据题目给出的求法,得出GD是AC的一半,然后按(2)的方法,通过延长AF来得出DF是(BC-AB)的一半,由此可得出FG=
 (BC+AC-AB).
(BC+AC-AB).解答:
 解:(1)猜想结果:如图结论为FG=
解:(1)猜想结果:如图结论为FG= (AB+AC-BC)
(AB+AC-BC)证明:分别延长AG、AF交BC于H、K,
在△BAF和△BKF中,
∵
 ,
,∴△BAF≌△BKF(ASA),
∴AF=KF,AB=KB
同理可证,AG=HG,AC=HC
∴FG=
 HK
HK又∵HK=BK-BH=AB+AC-BC
∴FG=
 (AB+AC-BC)
(AB+AC-BC)(2)图3的结论为FG=
 (BC+AC-AB).
(BC+AC-AB).证明:分别延长AG、AF交BC或延长线于H、K
在△BAF和△BKF中,

∵
 ,
,∴△BAF≌△BKF(ASA),
∴AF=KF,AB=KB
同理可证,AG=HG,AC=HC,
∴FG=
 KH
KH又∵KH=BC-BK+HC=BC+AC-AB.
∴FG=
 (BC+AC-AB).
(BC+AC-AB).点评:本题主要考查了直角三角形的性质,等腰三角形的性质,角平分线的性质以及全等三角形的判定等知识点.

练习册系列答案
相关题目
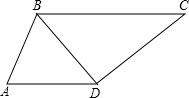 已知:如图,AD=BD=CD=m,AB=n,BC=p,BC∥AD,m、n为有理数.
已知:如图,AD=BD=CD=m,AB=n,BC=p,BC∥AD,m、n为有理数.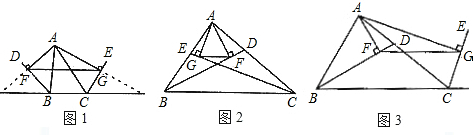
 已知:如图,BA=BD,BC=BE,∠ABD=∠CBE.
已知:如图,BA=BD,BC=BE,∠ABD=∠CBE. 已知:如图,AB⊥BD,CD⊥BD,AD=BC.求证:
已知:如图,AB⊥BD,CD⊥BD,AD=BC.求证: 已知:如图,AC=BD,AD⊥AC,BC⊥BD.求证:AD=AC.
已知:如图,AC=BD,AD⊥AC,BC⊥BD.求证:AD=AC.