题目内容
12.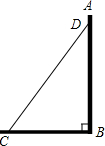 如图,将一长为6米的梯子CD斜靠在墙面上,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与地面的距离BD的长为( )米.
如图,将一长为6米的梯子CD斜靠在墙面上,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与地面的距离BD的长为( )米.| A. | 6cos55° | B. | $\frac{6}{sin55°}$ | C. | 6sin55° | D. | $\frac{6}{cos55°}$ |
分析 在Rt△BCD中,根据∠BCD=55°,CD=6米,解直角三角形求出BD的长度即可.
解答 解:在Rt△BCD中,
∵∠DBC=90°,∠BCD=55°,CD=6米,
∴BD=CD×sin∠BCD=6sin55°.
故选C.
点评 本题考查了解直角三角形的应用的知识,解答本题的关键是根据已知条件构造直角三角形并利用解直角三角形的知识求解,难度适中.

练习册系列答案
相关题目
20. 如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
 如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
4.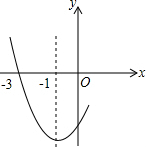 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ②③④ |
1. 如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )
如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )
 如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )
如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )| A. | 25° | B. | 24° | C. | 28° | D. | 22° |
2.cos60°的算术平方根等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{3}$ |
 若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )
若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )



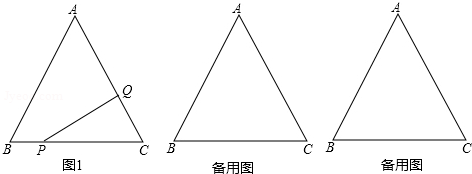
 园艺师从土地上收集了许多大理石的边角料,准备给公共绿地的通道铺地面,其中最多的一种边角材料形状如图所示,你能否用这种边角料铺满地面?如果能,请设计出至少两种方案.
园艺师从土地上收集了许多大理石的边角料,准备给公共绿地的通道铺地面,其中最多的一种边角材料形状如图所示,你能否用这种边角料铺满地面?如果能,请设计出至少两种方案.