题目内容
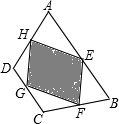如图已知：四边形ABCD的面积为60cm2，点E，F，G，H分别为四边形各边中点，则四边形EFGH的面积为________cm2．
30
分析：阴影部分面积等于四边形ABCD的面积减去4个空白三角形的面积，可利用相似求得4个空白三角形的面积，进而求解．
解答：连接BD，AC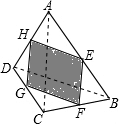
∵E，F，G，H分别为四边形各边中点
∴△AHE∽△ADB，相似比为
，面积比为
．
∴S△ADB=4S△AHE
同理可得，S△ADC=4S△HDG，S△BCD=4S△GCF，S△ACB=4S△EFB
∴S△ADB+S△ADC+S△BCD+S△ACB=2S四边形ABCD=4S△AHE+4S△HDG+4S△GCF+4S△EFB
∴S△AHE+S△HDG+S△GCF+S△EFB=S四边形ABCD
∴S四边形EFGH=S四边形ABCD-S△AHE+S△HDG+S△GCF+S△EFB=S四边形ABCD=×60=30cm．
点评：解答此题的关键是利用三角形的中位线定理及相似三角形的性质解答．
分析：阴影部分面积等于四边形ABCD的面积减去4个空白三角形的面积，可利用相似求得4个空白三角形的面积，进而求解．
解答：连接BD，AC
∵E，F，G，H分别为四边形各边中点
∴△AHE∽△ADB，相似比为
，面积比为．∴S△ADB=4S△AHE
同理可得，S△ADC=4S△HDG，S△BCD=4S△GCF，S△ACB=4S△EFB
∴S△ADB+S△ADC+S△BCD+S△ACB=2S四边形ABCD=4S△AHE+4S△HDG+4S△GCF+4S△EFB
∴S△AHE+S△HDG+S△GCF+S△EFB=
S四边形ABCD∴S四边形EFGH=S四边形ABCD-S△AHE+S△HDG+S△GCF+S△EFB=
S四边形ABCD=×60=30cm．点评：解答此题的关键是利用三角形的中位线定理及相似三角形的性质解答．
练习册系列答案
阅读快车系列答案
相关题目
=90
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
=90
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.