题目内容
用加减法解方程组
解:②×2,得6x-2y=-2③,
③+①得,7x=7,
x=1,
把x=1代入①,得1+2y=9,
2y=8,
y=4,
所以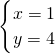 是原方程组的解.
是原方程组的解.
分析:用加减法解二元一次方程组时,必须使方程组中①②两方程所含同一个未知数的系数相同或互为相反数,现在该方程组不具备这个条件,所以我们要想办法转化成这样的条件.
方法一:观察x的系数:②中x的系数是①中的3倍,所以可得①×3,使x的系数相等,然后减去②,可消去x;
方程二:观察y的系数:①中y的系数是②中的2倍,所以可将②×2,便y的系数互为相反数,再与①相加可消去y,两种方法皆可达到消元的目的.
点评:方法点拨:用加减法解二元一次方程组时应当注意:
①当方程组比较复杂时,应先化简,如去分母、去括号、合并同类项等,将两方程化成ax+by=c的形式;
②当需将一未知数的系数扩大时,要根据等式的性质,一定要两边同乘以某一个倍数;
③在求出一未知数的值之后,可以将它代入化简后的方程组的任意一个方程中,求出第二个未知数的值;
④要想知道解是否正确,可将求得的解代入原方程组的两个方程加以检验.
③+①得,7x=7,
x=1,
把x=1代入①,得1+2y=9,
2y=8,
y=4,
所以
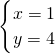 是原方程组的解.
是原方程组的解.分析:用加减法解二元一次方程组时,必须使方程组中①②两方程所含同一个未知数的系数相同或互为相反数,现在该方程组不具备这个条件,所以我们要想办法转化成这样的条件.
方法一:观察x的系数:②中x的系数是①中的3倍,所以可得①×3,使x的系数相等,然后减去②,可消去x;
方程二:观察y的系数:①中y的系数是②中的2倍,所以可将②×2,便y的系数互为相反数,再与①相加可消去y,两种方法皆可达到消元的目的.
点评:方法点拨:用加减法解二元一次方程组时应当注意:
①当方程组比较复杂时,应先化简,如去分母、去括号、合并同类项等,将两方程化成ax+by=c的形式;
②当需将一未知数的系数扩大时,要根据等式的性质,一定要两边同乘以某一个倍数;
③在求出一未知数的值之后,可以将它代入化简后的方程组的任意一个方程中,求出第二个未知数的值;
④要想知道解是否正确,可将求得的解代入原方程组的两个方程加以检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用加减法解方程组
,下列解法错误的是( )
|
| A、①×3-②×2,消去x |
| B、①×2-②×3,消去y |
| C、①×(-3)+②×2,消去x |
| D、①×2-②×(-3),消去y |
用加减法解方程组
中,消x用法,消y用法( )
|
| A、加,加 | B、加,减 |
| C、减,加 | D、减,减 |