Question

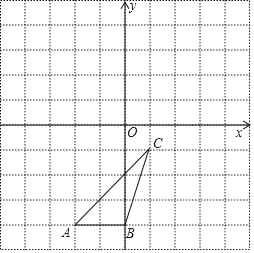
【题目】如图，△ABC各顶点的坐标分别是A（﹣2，﹣4），B（0，﹣4），C（1，﹣1）．

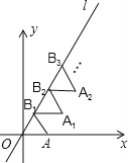
（1）在图中画出△ABC关于原点对称的△A1B1C1；

（2）在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2；

（3）在（2）的条件下，求点A运动路径长．

Answer 1

【答案】（1）（2）见作图；（3）.

【解析】分析：

（1）连AO延长至A1，使OA1=OA，得到点A1，同法作出点B1、C1，再顺次连接A1、B1、C1三点即可得到所求三角形；

（2）连接OA，把OA逆时针旋转90°得到OA2，得到点A2，同法作出点B2、C2，再顺次连接A2、B2、C2三点即可得到所求三角形；

（3）观察图形，由勾股定理易得OA=，结合∠AOA2=90°，由弧长公式计算出的长度即可.

详解：

（1）如图1，△A1B1C1为所求三角形；

（2）如图2，△A2B2C2为所求三角形；

（3）由图可得：OA=，

又∵∠AOA2=90°，

∴点A运动路径长为．