题目内容
 如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为________.
如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为________.
 +
+
分析:先利用扇形的面积公式计算出弓形AC的面积,这样就得到由弧AC,弧AB,弧BC所围成的图形面积和由弧AC,弧AD,弧DC所围成的图形面积,而三个圆所覆盖的图形面积=三个圆的面积-三个由弧AC,弧AB,弧BC所围成的图形面积-2个由弧AC,弧AD,弧DC所围成的图形面积.
解答:
 解:如图,连AD,CD,则△ADC是边长为1的等边三角形,
解:如图,连AD,CD,则△ADC是边长为1的等边三角形,∴弓形AC的面积=扇形BAC的面积-△ABC的面积,
=
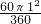 -
- •12
•12=
 -
- ,
,∴由弧AC,弧AB,弧BC所围成的图形面积=3×(
 -
- )+
)+ =
= -
- .
.∴由弧AC,弧AD,弧DC所围成的图形面积=
 •12+(
•12+( -
- )=
)= ;
;∴三个圆所覆盖的图形面积=3•π•12-3×
 -2×(
-2×( -
- )=
)= +
+ .
.故答案为:
 +
+ .
.点评:本题考查了扇形的面积公式:l=
 .也考查了等边三角形的性质以及利用规则的图形面积的和差表示不规则的几何图形面积的计算方法.
.也考查了等边三角形的性质以及利用规则的图形面积的和差表示不规则的几何图形面积的计算方法. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
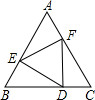 如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )
如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
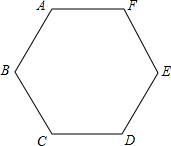 已知:如图,边长为a的正六边形ABCDEF.
已知:如图,边长为a的正六边形ABCDEF.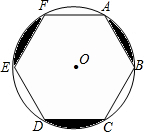 如图,边长为2的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为
如图,边长为2的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为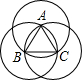 如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为
如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为 如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )
如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )