题目内容
20.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(万件)之间的关系如表:| x(元) | 10 | 15 | 20 | … |
| y(件) | 30 | 25 | 20 | … |
(1)求出日销售量y(万件)与销售价x(元)的函数关系式;
(2)若每日的销售利润为w(万元),要使每日的销售利润最大,每件产品的销售价应为多少元?此时每日销售利润是多少?
分析 (1)根据题意可以得到y与x的函数关系;
(2)根据题意可以得到w关于x的函数关系式,然后化为顶点式即可解答本题.
解答 解:(1)设此一次函数的解析式为y=kx+b,
$\left\{\begin{array}{l}{10k+b=30}\\{15k+b=25}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-1}\\{b=40}\end{array}\right.$,
即日销售量y(万件)与销售价x(元)的函数关系式是y=-x+40;
(2)由题意可得,
w=(x-10)(-x+40)=-(x-25)2+225,
∴当x=25时,w取得最大值,此时w=225,
即每件产品的销售价应为25元,此时每日销售利润是225万元.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
8.当x=-2时,代数式x-3的值是( )
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
10.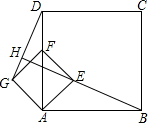 四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
 四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )| A. | $4\sqrt{2}$ | B. | 16 | C. | $\frac{{8\sqrt{10}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{2}$ |
 如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方4.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高3.12m.
如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方4.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高3.12m.