Question

（12分）探究：

在矩形ABCD中，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．

（1）如图1，求证：ME=MF；

（2）如图2，点G是线段BC上一点，连接GE、GF、GM，若△EGF是等腰直角三角形，∠EGF=90°，求AB：AD的值；

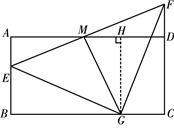
（3）如图3，点G是线段BC延长线上一点，连接GE、GF、GM，若△EGF是等边三角形，直接写出AB、AD满足的数量关系.

 

Answer 1

见解析

【解析】

试题分析：（1）根据ABCD是矩形，得出∠EAM=∠FDM=90°，根据AM=DM，∠AME=∠FMD证出△AEM≌△DFM，即可得出ME=FM；（2）过点G作GH⊥AD于H，根据条件证出△AEM≌△HMG，得出GH=AM，因为点M是中点，所以AB=HG=AM=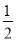AD，所以AB:AD=2:1；（3）过点G作GH⊥AD交AD延长线于点H，连接MG，则∠GHM=∠A，根据△GEF是等边三角形，得出EM=FM，GM⊥EF，∠AME+∠GMH=90°，根据∠AME+∠AEM=90°，得出∠GMH=∠AEM，证出△AEM∽△HMG，所以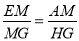，又根据题意可知∠MGF=∠EGM=30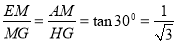°,所以，所以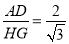,AB=HG,所以AB=．

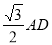试题解析：（1）证明：在矩形ABCD中，∠A＝∠FDM＝90°.又∵AM＝DM，∠AME＝∠DMF，

∴△AME≌△DMF，∴ME=MF.

（2）【解析】
如图，过点G作GH⊥AD于点H.

∴四边形ABGH是矩形.∵△EGF是等腰直角三角形，由（1）得，ME=MF，∴ME=MG，∠EMG＝90°.

∴∠AME+∠DMG＝∠HGM+∠DMG=90°,∴∠AME＝∠HGM.又∵∠A＝∠MHG，∴△AME≌△HGM

∴AM=HG.∴AB=HG=AM=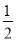AD∴AD=2AB∴AB:AD=2:1

（3）AB=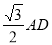

考点：1.矩形的性质；2.三角形的全等与相似；3.等腰三角形的性质；4.等边三角形的性质.