题目内容
1.已知,如图1,△ABC和△EDC都是等边三角形,点D,E分别在BC,AC上.(1)填空:∠AED=∠CDE=120度;
(2)求证:AD=BE;
(3)如图将图1中的△EDC沿BC所在直线翻折(如图2所示),其它条件不变,(2)中结论是否成立?请说明理由.
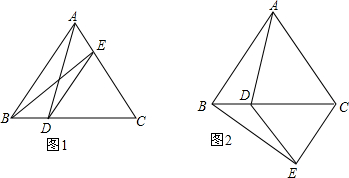
分析 (1)由△DCE为等边三角形可知∠CDE=∠CED=60°,然后由邻补角的定义可知∠AED=∠CDE=120°;
(2)证明△BDE和△AED全等即可;
(3)由等边三角形的性质可知:AC=BC,DC=EC,∠ACB=∠BCE,从而可证明△ACD≌△BCE,从而可得到AD=BE.
解答 (1)解:∵△EDC都是的等边三角形,
∴∠CDE=∠CED=60°.
∴∠AED=∠CDE=120°.
故答案为:∠CDE;120.
(2)证明:∵△ABC和△EDC都是等边三角形,
∴AC=BC,EC=DC.
∴AC-EC=BC-DC即AE=BD.
在△AED和△BDE中,
$\left\{\begin{array}{l}{AE=BD}\\{∠AED=∠BDE}\\{ED=DE}\end{array}\right.$,
∴△AED≌△BDE(SAS).
∴AD=DE.
(3)AD=BE仍成立.
理由:∵△ABC和△CDE都是等边三角形,
∴AC=BC,EC=DC,∠ACD=∠BCE=60°.
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{EC=DC}\end{array}\right.$,
∴△ACD≌△BCE.
∴AD=BE.
点评 本题主要考查的是等边三角形的性质、全等三角形的性质和判定,掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
12.已知a<b,c是有理数,下列各式中正确的是( )
| A. | ac2<bc2 | B. | c-a<c-b | C. | a-c<b-c | D. | $\frac{a}{c}<\frac{b}{c}$ |
9.下列条件中一定能使△ABC≌△DEF成立的是( )
| A. | 两边对应相等 | B. | 面积相等 | C. | 三边对应相等 | D. | 周长相等 |
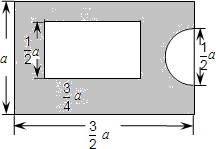 一个长方形的娱乐场所的宽是a米,长是宽的1.5倍,其设计如图所示,其中半圆形休息区和长方形游泳池以外是绿地(如图阴影部分所示),请计算绿地面积是多少?
一个长方形的娱乐场所的宽是a米,长是宽的1.5倍,其设计如图所示,其中半圆形休息区和长方形游泳池以外是绿地(如图阴影部分所示),请计算绿地面积是多少? 如图是某时刻在镜子中看到准确时钟的情况,则实际时间是7点20分(或7:20).
如图是某时刻在镜子中看到准确时钟的情况,则实际时间是7点20分(或7:20).