题目内容
已知直线l1:y=-4x+5和直线l2:y=| 1 | 2 |
(1)求两条直线l1和l2的交点坐标;
(2)求两条直线l1和l2与x轴围成的三角形的面积.
分析:(1)要求两条直线l1和l2的交点坐标把他们解析式组成方程组解之即可得到交点坐标;
(2)如图,设两条直线l1和l2与x轴的交点为A,B,则容易求出A(8,0),B(
,0),然后根据已知坐标即可求出两条直线l1和l2与x轴围成的三角形的面积.
(2)如图,设两条直线l1和l2与x轴的交点为A,B,则容易求出A(8,0),B(
| 5 |
| 4 |
解答: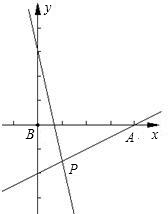 解:(1)设两条直线l1和l2的交点坐标为P(x,y),
解:(1)设两条直线l1和l2的交点坐标为P(x,y),
依题意得
,
解得
,
即P(2,-3);
(2)如图,设两条直线l1和l2与x轴的交点为A,B
则A(8,0),B(
,0),
∴S△PAB=
×(8-
)×3=
.
 解:(1)设两条直线l1和l2的交点坐标为P(x,y),
解:(1)设两条直线l1和l2的交点坐标为P(x,y),依题意得
|
解得
|
即P(2,-3);
(2)如图,设两条直线l1和l2与x轴的交点为A,B
则A(8,0),B(
| 5 |
| 4 |
∴S△PAB=
| 1 |
| 2 |
| 5 |
| 4 |
| 81 |
| 8 |
点评:此题主要考查平面直角坐标系中交点坐标和图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.

练习册系列答案
相关题目
 如图,已知直线l1:y=2x+3,直线l2:y=-x+5,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A.
如图,已知直线l1:y=2x+3,直线l2:y=-x+5,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A. (2013•济南)已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值等于( )
(2013•济南)已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值等于( )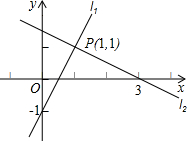 象所提供的信息回答下列问题:
象所提供的信息回答下列问题: 如图,已知直线l1,l2和△ABC,且l1⊥l2于点O.点A在l1上,点B、点C在l2上.
如图,已知直线l1,l2和△ABC,且l1⊥l2于点O.点A在l1上,点B、点C在l2上. 阅读下面的材料:
阅读下面的材料: