Question

（2013•济南）已知直线l₁∥l₂∥l₃∥l₄，相邻的两条平行直线间的距离均为h，矩形ABCD的四个顶点分别在这四条直线上，放置方式如图所示，AB=4，BC=6，则tanα的值等于（　　）

• A．

  2

  3

• B．

  3

  4

• C．

  4

  3

• D．

  3

  2

Answer 1

分析：过点C作CE⊥l₄于点E，延长EC交l₁于点F，根据同角的余角相等求出∠α=∠DCF，利用两角对应相等的两三角形相似证明△BEC∽△CFD，再由相似三角形对应边成比例可得BE=

3

2

h，然后在Rt△BCE中利用锐角的正切值等于对边比邻边列式计算即可得解．

解答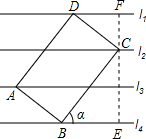：解：如图，过点C作CE⊥l₄于点E，延长EC交l₁于点F．
在矩形ABCD中，∠BCD=90°，
∵∠α+∠BCE=90°，∠BCE+∠DCF=180°-90°=90°，
∴∠α=∠DCF，
又∵∠BEC=∠CFD=90°，
∴△BEC∽△CFD，
∴

BE

CF

=

BC

CD

，即

BE

h

=

6

4

，
∴BE=

3

2

h．
在Rt△BCE中，∵∠BEC=90°，
∴tanα=

CE

BE

=

2h

3 2 h

=

4

3

．
故选C．

点评：本题考查了相似三角形的判定与性质，矩形的性质，锐角三角形函数的定义，作辅助线，构造出相似三角形以及∠α所在的直角三角形是解题的关键．