题目内容
【题目】已知C是线段AB垂直平分线m上一动点,连接AC,以AC为边作等边三角形ACD,点D在直线AB的上方,连接DB与直线m交于点E,连接BC,AE.
(1)如图1,点C在线段AB上.
①根据题意补全图1;
②求证:∠EAC=∠EDC;
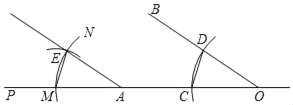
(2)如图2,点C在直线AB的上方, 0°<∠CAB<30°,用等式表示线段BE,CE,DE之间的数量关系,并证明.

【答案】(1)①补全图形见解析;②证明见解析;(2)BE=CE+DE,证明见解析.
【解析】
(1)①根据题意补全图形即可;②根据垂直平分线的性质可得EA=EB,CA=CB,根据等边三角形的性质可得CA=CD,因此CD=CB,即可证得∠EDC=∠B;(2)如图,在EB上截取EF,使EF=CE,连接CF.根据垂直平分线的性质以及等边三角形的性质可推出∠EDC=∠EAC,又因为∠1=∠2,可得∠DEA=60°,所以∠AEB=120°,进而可推出△CEF是等边三角形,因此△CDF≌△CBE,故BE=DF=CE+DE.
(1)①补全图形如图所示.

②∵直线m是AB的垂直平分线,
∴EA=EB,CA=CB.
∴∠EAC=∠B.
∵△ACD是等边三角形,
∴CA=CD.
∴CD=CB.
∴∠EDC=∠B.
∴∠EAC=∠EDC.
(2)BE=CE+DE.

如图,在EB上截取EF,使EF=CE,连接CF.
∵直线m是AB的垂直平分线,
∴EA=EB,CA=CB.
∴∠EAB=∠EBA,∠CAB=∠CBA.
∴∠EAC=∠EBC.
∵△ACD是等边三角形,
∴CA=CD,∠ACD=60°.
∴CD=CB.
∴∠EDC=∠EBC.
∴∠EDC=∠EAC.
∵∠1=∠2,
∴∠DEA=∠ACD=60°.
∴∠AEB=120°.
∵EA=EB,m⊥AB,
∴∠AEC=∠BEC=60°.
∴△CEF是等边三角形.
∴∠CEF=∠CFE=60°.
∴△CDF≌△CBE.
∴DF=BE.
∴BE=CE+DE.

【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
户 数 | 1 | 1 | 2 | 4 |
这20个家庭的年平均收入为 万元;
(2)样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平.