题目内容
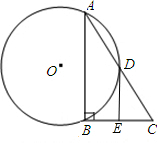 已知:AB是⊙O的弦,D是
已知:AB是⊙O的弦,D是 | AB |
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=EC,求sinC.
分析:(1)连接BD,根据圆周角定理求出∠A=∠ABD,即AD=BD,再根据直角三角形的性质通过等量代换即可求出△BCD是等腰三角形,根据等腰三角形的性质即可解答.
(2)连接OD交AB于F,根据切线的性质可知OD⊥DE,由D是
的中点可知AB⊥OD,四边形FBED为矩形,再根据直角三角形的性质可求出△BDC是等腰三角形,可求出BE=EC=DE,∠C=45°,再根据特殊角的三角函数值解答即可.
(2)连接OD交AB于F,根据切线的性质可知OD⊥DE,由D是
 |
| AB |
解答: (1)证明:连BD,
(1)证明:连BD,
∵
=
,
∠A=∠ABD,
∴AD=BD;(2分)
∵∠A+∠C=90°,∠DBA+∠DBC=90°,
∴∠C=∠DBC,
∴BD=DC,
∴AD=DC.(4分)
(2)解:连接OD交AB于F,
∵DE为⊙O切线,
∴OD⊥DE;(5分)
∵
=
,OD过圆心,
∴OD⊥AB;
又∵AB⊥BC,
∴四边形FBED为矩形,
∴DE⊥BC;(6分)
又∵BD=DC,
∴BE=EC=DE,
∴△BCD为等腰直角三角形,
∴∠C=45°;(7分)
∴sinC=
.(8分)
 (1)证明:连BD,
(1)证明:连BD,∵
 |
| BD |
 |
| AD |
∠A=∠ABD,
∴AD=BD;(2分)
∵∠A+∠C=90°,∠DBA+∠DBC=90°,
∴∠C=∠DBC,
∴BD=DC,
∴AD=DC.(4分)
(2)解:连接OD交AB于F,
∵DE为⊙O切线,
∴OD⊥DE;(5分)
∵
 |
| BD |
 |
| AD |
∴OD⊥AB;
又∵AB⊥BC,
∴四边形FBED为矩形,
∴DE⊥BC;(6分)
又∵BD=DC,
∴BE=EC=DE,
∴△BCD为等腰直角三角形,
∴∠C=45°;(7分)
∴sinC=
| ||
| 2 |

点评:此类题目比较复杂,解答此类题目的关键是作出辅助线,根据切线的性质及圆周角定理解答.

练习册系列答案
相关题目
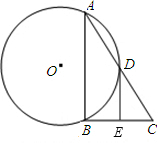 已知:AB是⊙O的弦,D是
已知:AB是⊙O的弦,D是 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是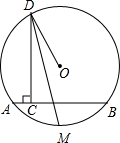 如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.