题目内容
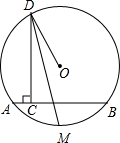如图，已知：AB是⊙O的弦，D为⊙O上一点，DC⊥AB于C，DM平分∠CDO．求证：M是弧AB的中点．分析：连接OM，首先证明∠CDM=∠OMD，进而求出OM⊥AB，利用垂径定理求出即可．
解答：
解：连接OM
∵OD=OM，
∴∠ODM=∠OMD，
∵DM平分∠ODC，
∴∠ODM=∠CDM，
∴∠CDM=∠OMD，
∴CD∥OM，
∵CD⊥AB，
∴OM⊥AB，
∴弧AM=弧BM，
即点M为劣弧AB的中点．
解：连接OM∵OD=OM，
∴∠ODM=∠OMD，
∵DM平分∠ODC，
∴∠ODM=∠CDM，
∴∠CDM=∠OMD，
∴CD∥OM，
∵CD⊥AB，
∴OM⊥AB，
∴弧AM=弧BM，
即点M为劣弧AB的中点．
点评：此题主要考查了垂径定理以及平行的线的判定和圆周角定理，此题难度不大，得出OM⊥AB是解题关键．
练习册系列答案
备战中考寒假系列答案
相关题目
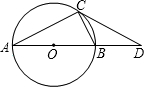如图，已知：AB是⊙O的直径，BD=OB，∠CAB=30°，请根据已知条件和所给图形，写出8个正确的结论（除AO=OB=BD外）．
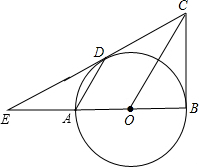CD的延长线的交点．
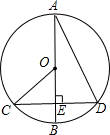如图，已知：AB是⊙O的直径，CD⊥AB于E，连接AD、OC．
如图，已知：AB是⊙O的弦，C是AB上的点，AC=4、BC=1、OC=2，则⊙O的半径是