题目内容
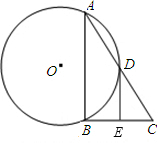 已知:AB是⊙O的弦,D是
已知:AB是⊙O的弦,D是 | AB |
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=EC,求∠C.
分析:(1)根据D是弧AB的中点,可以证得AD=BD,然后根据等角对等边,即可证得BD=CD,从而求证;
(2)证明△DCE是等腰直角三角形,即可求解.
(2)证明△DCE是等腰直角三角形,即可求解.
解答: (1)证明:连接BD,
(1)证明:连接BD,
∵D是
的中点.
∴AD=BD,
∴∠A=∠ABD,
∵∠A+∠C=∠ABD+∠DBC=90°,
∴∠DBC=∠C,
∴BD=CD,
∴AD=DC;
(2)解:∵DE是○O的切线,
∴OD⊥DE,
∵D是
的中点.
∴OD⊥AB,
∴AB∥DE,
∴DE⊥BC,
又∵DE=EC,
∴∠C=45°.
 (1)证明:连接BD,
(1)证明:连接BD,∵D是
 |
| AB |
∴AD=BD,
∴∠A=∠ABD,
∵∠A+∠C=∠ABD+∠DBC=90°,
∴∠DBC=∠C,
∴BD=CD,
∴AD=DC;
(2)解:∵DE是○O的切线,
∴OD⊥DE,
∵D是
 |
| AB |
∴OD⊥AB,
∴AB∥DE,
∴DE⊥BC,
又∵DE=EC,
∴∠C=45°.
点评:本题主要考查了切线的性质,以及弧与弦之间的关系,正确证明△DCE是解题的关键.

练习册系列答案
相关题目
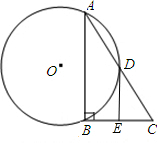 已知:AB是⊙O的弦,D是
已知:AB是⊙O的弦,D是 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是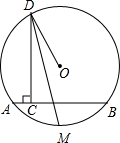 如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.