题目内容
【题目】如图,抛物线y=ax2﹣5ax﹣4交x轴于A,B两点(点A位于点B的左侧),交y轴于点C,过点C作CD∥AB,交抛物线于点D,连接AC、AD,AD交y轴于点E,且AC=CD,过点A作射线AF交y轴于点F,AB平分∠EAF.
(1)此抛物线的对称轴是 ;
(2)求该抛物线的解析式;
(3)若点P是抛物线位于第四象限图象上一动点,求△APF面积S△APF的最大值,以及此时点P的坐标;
(4)点M是线段AB上一点(不与点A,B重合),点N是线段AD上一点(不与点A,D重合),则两线段长度之和:MN+MD的最小值是 .

【答案】(1)直线x=![]() ;(2)抛物线解析式为y=
;(2)抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣4;(3)当x=4时,S△APF的最大值为
x﹣4;(3)当x=4时,S△APF的最大值为![]() ,此时P点坐标为(4,﹣
,此时P点坐标为(4,﹣![]() );(4)
);(4)![]() .
.
【解析】分析:(1)直接利用抛物线的对称轴方程求解;(2)先确定C(0,4)再利用对称性得到D(5,-4),从而得到CD=AC=5,然后求出A点的坐标,再把A点坐标代入y=ax-5ax-4中求出a即可;(3)作PQ∥y轴交AF于Q,如图1,先利用待定系数法确定直线AD的解析式为y=﹣![]() x﹣
x﹣![]() 得到E(0,-
得到E(0,-![]() ),再根据等腰三角形的三线合一确定F(0,
),再根据等腰三角形的三线合一确定F(0,![]() ),则易得直线AF的解析式为y=
),则易得直线AF的解析式为y=![]() ,设P(x,
,设P(x,![]() -4)(0<x<8=,则Q(x,
-4)(0<x<8=,则Q(x,![]() ) ,所以PQ=
) ,所以PQ= ![]() ,然后利用三角形面积公式,根据
,然后利用三角形面积公式,根据![]() 可表示出
可表示出![]() ,最后利用二次函数的性质解决问题;
,最后利用二次函数的性质解决问题;
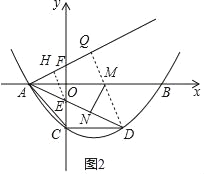
(4)作DQ⊥AF于Q,交x轴于M,作MN⊥AD于N,EH⊥AF于H,如图2,利用两点之间线段最短和垂线段最短判断此时MN+MD的值最小,再利用面积法求出EH,然后利用平行线分线段成比例定理计算DQ即可.
详解:(1)抛物线的对称轴为直线x=﹣![]() =
=![]() ;
;
(2)当x=0时,y=ax2﹣5ax﹣4=﹣4,则C(0,﹣4);
∵CD∥x轴,
∴点C与点D关于直线x=![]() 对称,
对称,
∴D(5,﹣4),CD=5,
∵AC=CD,
∴AC=5,
在Rt△AOC中,OA=![]() =3,
=3,
∴A(﹣3,0),
把A(﹣3,0)代入y=ax2﹣5ax﹣4得9a+15a﹣4=0,解得a=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(3)作PQ∥y轴交AF于Q,如图1,
当y=0时,![]() x2﹣
x2﹣![]() x﹣4=0,解得x1=﹣3,x2=8,则P(8,0),
x﹣4=0,解得x1=﹣3,x2=8,则P(8,0),
设直线AD的解析式为y=kx+b,
把A(﹣3,0),D(5,﹣4)代入得![]() ,解得
,解得![]() ,
,
∴直线AD的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
当x=0时,y=﹣![]() x﹣
x﹣![]() =﹣
=﹣![]() ,则E(0,﹣
,则E(0,﹣![]() ),
),
∵AB平分∠EAF,AO⊥EF,
∴OF=OE=![]() ,
,
∴F(0,![]() ),
),
易得直线AF的解析式为y=![]() x+
x+![]() ,
,
设P(x,![]() x2﹣
x2﹣![]() x﹣4)(0<x<8),则Q(x,
x﹣4)(0<x<8),则Q(x,![]() x+
x+![]() ),
),
∴PQ=![]() x+
x+![]() ﹣(
﹣(![]() x2﹣
x2﹣![]() x﹣4)=﹣
x﹣4)=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
∴S△APF=S△PAQ﹣S△PFQ=![]() 3PQ=﹣
3PQ=﹣![]() x2+2x+
x2+2x+![]() =﹣
=﹣![]() (x﹣4)2+
(x﹣4)2+![]() ,
,
当x=4时,S△APF的最大值为![]() ,此时P点坐标为(4,﹣
,此时P点坐标为(4,﹣![]() );
);
(4)作DQ⊥AF于Q,交x轴于M,作MN⊥AD于N,EH⊥AF于H,如图2,
∵AB平分∠EAF,
∴MQ=MN,
∴MN+MD=DQ,
∴此时MN+MD的值最小,
∵A(﹣3,0),E(0,﹣![]() ),D(5,﹣4),
),D(5,﹣4),
∴AE=![]() =
=![]() ,AD=
,AD=![]() =4
=4![]() ,
,
∵![]() OAEF=
OAEF=![]() EHAF,
EHAF,
∴EH=![]() =
=![]() ,
,
∵EH∥DQ,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DQ=![]() ,
,
即MN+MD的最小值是![]() .
.
故答案为直线x=![]() ;
;![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案







