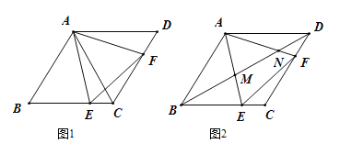
题目内容
【题目】在![]() 中,
中, ![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折线,将
为折线,将![]() 翻折,设所得的
翻折,设所得的![]() 与梯形
与梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
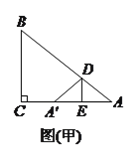
(![]() )如图(甲),若
)如图(甲),若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的值为__________.
的值为__________.
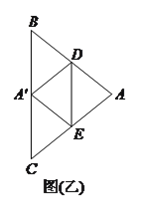
(![]() )如图(乙),若
)如图(乙),若![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,则
中点,则![]() 的值为__________.
的值为__________.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
①求![]() 与
与![]() 的函数解析式.
的函数解析式.
②![]() 是否有最大值,若有,求出
是否有最大值,若有,求出![]() 的最大值;若没有,请说明理由.
的最大值;若没有,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①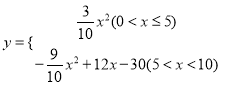 ;②当
;②当![]() 时,
时, ![]() 值最大,最大值为
值最大,最大值为![]() .
.
【解析】试题分析:(1)本题需先根据已知条件得出AC的长,再根据DE∥BC得出△ADE∽△ABC,再根据面积之比等于相似比的平方即可求出结果.
(2)本题需先根据已知条件得出BC边上的高的值和S△ABC的值,再根据D为AB中点和DE∥BC,即可得出△ADE∽△ABC,最后根据面积之比等于相似比的平方即可求出结果;
(3)本题需先作AH⊥BC于点H,根据已知条件得出AH和S△ABC的值,再分两种情况0<x≤5时和当5<x<10进行讨论,分别求出![]() 和
和![]() 的值,即可求出y的最大值.
的值,即可求出y的最大值.
解:(![]() )∵
)∵![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴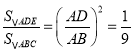 ,∴
,∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() 边上的高为
边上的高为![]() ,∴
,∴![]() ,∵
,∵![]() 为
为![]() 的中点,
的中点, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴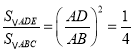 ,∴
,∴![]() ,∴
,∴![]() .
.
(![]() )如图a,作
)如图a,作![]() 于点
于点![]() ,在
,在![]() 中,∵
中,∵![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,当
,当![]() 落在
落在![]() 上时,
上时, ![]() 为
为![]() 的中点:
的中点:

即![]() 故分以下两种情况讨论:
故分以下两种情况讨论:
①当![]() 时,如图b,∵
时,如图b,∵![]() ,∴
,∴![]() ,∴
,∴ ,∴
,∴![]() ,即
,即![]() ,∴当
,∴当![]() 时,
时, ![]() .
.
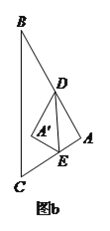
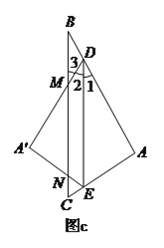
②当![]() 时,如图c,设
时,如图c,设![]() ,
, ![]() 分别交
分别交![]() 于
于![]() ,
, ![]() ,由折叠可知,
,由折叠可知, ![]() ,∴
,∴![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,由①同理得
,由①同理得![]() ,又
,又![]() ,∴
,∴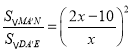 ,∴
,∴![]() ,∴
,∴![]()
![]()
∵![]() ,且当
,且当![]() 时满足
时满足![]() ,∴
,∴![]() 。
。
∴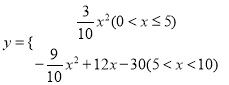
当![]() 时,
时, ![]() 值最大,最大值为
值最大,最大值为![]() .
.

练习册系列答案
相关题目