题目内容
19.已知一次函数y=mx+n的图象过点A(-1,4),且与y轴交点的纵坐标是-2,这个函数的表达式是y=-6x-2.分析 与y轴交点的纵坐标是-2,即交点坐标是(0,-2),则函数经过点(-1,4)与(0,-2),利用待定系数法即可求得函数的解析式.
解答 解:根据题意得:$\left\{\begin{array}{l}{-m+n=4}\\{n=-2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=-6}\\{n=-2}\end{array}\right.$
则函数的解析式是:y=-6x-2.
故答案为y=-6x-2.
点评 考查了待定系数法求函数的解析式.先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.

练习册系列答案
相关题目
14.已知关于二次函数y=(x-2011)2+(x-2012)2+(x-2013)2+(x-2014)2+(x-2015)2的下列说法:①当x>2013时,y随x的增大而增大;②对称轴是x=2013;③顶点坐标为(2013,10);④开口向下;⑤函数的最大值是2013,其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.若x>0,y>0,则化简x$\sqrt{xy}$÷y$\sqrt{\frac{x}{y}}$×$\sqrt{\frac{y}{x}}$等于( )
| A. | $\frac{y}{x}$$\sqrt{xy}$ | B. | $\frac{x}{y}$$\sqrt{xy}$ | C. | $\sqrt{xy}$ | D. | xy$\sqrt{xy}$ |
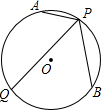 如图,点A、B是⊙O上的定点,且圆周角∠APB=120°,∠APB的角平分线交⊙O于点Q.(1)当点P在$\widehat{AB}$上运动(不与点A、B重合)时,问点Q移动吗?试说明理由.
如图,点A、B是⊙O上的定点,且圆周角∠APB=120°,∠APB的角平分线交⊙O于点Q.(1)当点P在$\widehat{AB}$上运动(不与点A、B重合)时,问点Q移动吗?试说明理由.