题目内容
16.(1)化简:($\frac{b}{a-3}$+$\frac{3b}{9-{a}^{2}}$)÷$\frac{ab}{{a}^{2}-6a+9}$(2)解不等式组:$\left\{\begin{array}{l}{3(x+2)>2x+5(1)}\\{\frac{2x-1}{3}≥x-\frac{3}{2}(2)}\end{array}\right.$,并写出不等式组所有的整数解.
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,确定出所有整数解即可.
解答 解:(1)原式=$\frac{b(a+3)-3b}{(a+3)(a-3)}$•$\frac{(a-3)^{2}}{ab}$=$\frac{a-3}{a+3}$;
(2)由(1)解得:x>-1;
由(2)解得:x≤3.5,
∴不等式组的解集为-1<x≤3.5,
则不等式组的所有整数解为0,1,2,3.
点评 此题考查了分式的混合运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
11.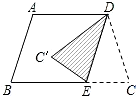 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )
 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )| A. | 72° | B. | 54° | C. | 36° | D. | 30° |
8.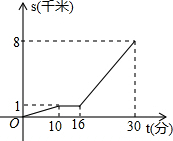 小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
 小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )| A. | 他家到公交车站台为1千米 | B. | 他等公交车的时间为6分钟 | ||
| C. | 他步行的速度100米/分钟 | D. | 公交车的速度是350米/分钟 |
14.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}x=2y+1\\ y=3-z\end{array}\right.$ | B. | $\left\{\begin{array}{l}xy=12\\ x+y=7\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | D. | $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=2\\ 3x-2y=4\end{array}\right.$ |
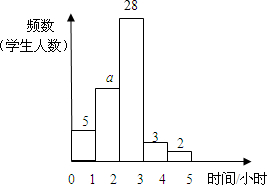 某中学九年级(1)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
某中学九年级(1)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
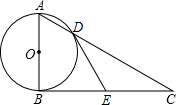 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接BD、DE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接BD、DE.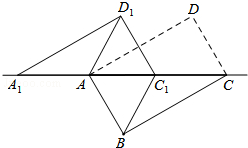 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论: