题目内容
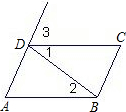 推理填空:
推理填空:
(1)如图,①若∠1=∠2
则______∥______
若∠DAB+∠ABC=180°
则______∥______
②当______∥______时
∠C+∠ABC=180°______
③当______∥______时
∠3=∠A______
(2)如图,D是AB上的一点,E是AC上一点,∠ADE=70°,∠B=70°,∠BCD=17°.求∠EDC的度数.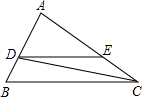
解:因为∠ADE=70°,∠B=70°
所以______∥______
所以∠BCD=______
因为∠BCD=17°
所以∠EDC=______.
解:(1)如图,①若∠1=∠2
则 DC∥AB
若∠DAB+∠ABC=180°
则 AD∥BC
②当 DC∥AB时
∠C+∠ABC=180° 两直线平行,同旁内角互补
③当 DC∥AB时
∠3=∠A 两直线平行,同位角相等
(2)如图,D是AB上的一点,E是AC上一点,∠ADE=70°,∠B=70°,∠BCD=17°.求∠EDC的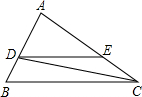 度数.
度数.
解:因为∠ADE=70°,∠B=70°
所以 DE∥BC
所以∠BCD=∠EDC
因为∠BCD=17°
所以∠EDC=17°.
分析:(1)根据平行线的判定定理,①内错角相等,两直线平行;同旁内角互补,两直线平行;②两直线平行,同旁内角互补;两直线平行,同位角相等;
和性质定理分别分析得出即可.
(2)根据平行线的判定得出,同位角相等两直线平行即可得出答案.
点评:此题主要考查了平行线的性质和判定定理的综合运用.灵活应用平行线的性质与判定是解决问题的关键.
则 DC∥AB
若∠DAB+∠ABC=180°
则 AD∥BC
②当 DC∥AB时
∠C+∠ABC=180° 两直线平行,同旁内角互补
③当 DC∥AB时
∠3=∠A 两直线平行,同位角相等
(2)如图,D是AB上的一点,E是AC上一点,∠ADE=70°,∠B=70°,∠BCD=17°.求∠EDC的
 度数.
度数.解:因为∠ADE=70°,∠B=70°
所以 DE∥BC
所以∠BCD=∠EDC
因为∠BCD=17°
所以∠EDC=17°.
分析:(1)根据平行线的判定定理,①内错角相等,两直线平行;同旁内角互补,两直线平行;②两直线平行,同旁内角互补;两直线平行,同位角相等;
和性质定理分别分析得出即可.
(2)根据平行线的判定得出,同位角相等两直线平行即可得出答案.
点评:此题主要考查了平行线的性质和判定定理的综合运用.灵活应用平行线的性质与判定是解决问题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 25、推理填空:
25、推理填空: 推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.
推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.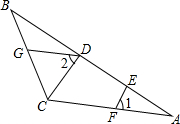 推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.
推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.