Question

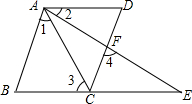
推理填空：已知：如图，DG∥AC，EF⊥AB，∠1=∠2．求证：CD⊥AB．
证明：∵DG∥AC （________）
∴∠2=∠________（________）
∵∠1=∠2（________）
∴∠1=∠________（等量代换）
∴EF∥CD（________）
∴∠AEF=∠________ （________）
∵EF⊥AB，∴∠AEF=90° （________）
∴∠ADC=90° （等量代换）
即CD⊥AB．

Answer 1

已知    ACD    两直线平行，内错角相等    已知    ACD    同位角相等，两直线平行    ADC    两直线平行，同位角相等    垂直定义
分析：根据平行线的判定方法与性质进行填空即可．
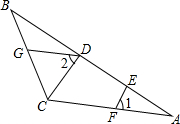
解答：证明：∵DG∥AC （已知）
∴∠2=∠ACD（两直线平行，内错角相等）
∵∠1=∠2（已知）
∴∠1=∠ACD（等量代换）
∴EF∥CD（同位角相等，两直线平行）
∴∠AEF=∠ADC（两直线平行，同位角相等）
∵EF⊥AB，∴∠AEF=90° （垂直定义）
∴∠ADC=90° （等量代换）
即CD⊥AB．
故答案为：已知；ACD；两直线平行，内错角相等；已知；ACD；同位角相等，两直线平行；ADC；两直线平行，同位角相等；垂直定义．
点评：本题考查了平行线的判定与性质，主要训练了逻辑推理的理论依据，是基础题，熟练掌握平行线的判定方法与性质是解题的关键．