题目内容
推理填空：
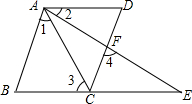
已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。
求证：AD∥BE。
证明：∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（等式的性质）
即∠ BAF =∠
∴∠3=∠ （ ）
∴AD∥BE（ 
）
 |
（每空1分）推理填空：
已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。
求证：AD∥BE。
证明：∵AB∥CD（已知）
∴∠4=∠BAF（两直线平行，同位角相等）
∵∠3=∠4（已知）
∴∠3=∠BAF（等量代换）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（等式的性质）
即∠ BAF =∠CAD
∴∠3=∠CAD（等量代换）
∴AD∥BE（内错角相等，两直线平行）
练习册系列答案
阅读快车系列答案
相关题目
25、推理填空：
推理填空：已知：如图，DG∥AC，EF⊥AB，∠1=∠2．求证：CD⊥AB．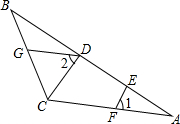
推理填空：已知：如图，DG∥AC，EF⊥AB，∠1=∠2．求证：CD⊥AB．