题目内容
 如图,已知⊙O的直径CD为2,
如图,已知⊙O的直径CD为2, 的度数为60°,点B是
的度数为60°,点B是 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为________.
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为________.

分析:作B关于CD的对称点E,则E正好在圆周上连接OA、OB、OE、AE,AE交CD于P,则AP+BP最短,根据
 的度数为60°,点B是
的度数为60°,点B是 的中点计算出,∠AOB=∠COB=30°,然后再证明△OAE是等腰直角三角形,再利用勾股定理可得答案.
的中点计算出,∠AOB=∠COB=30°,然后再证明△OAE是等腰直角三角形,再利用勾股定理可得答案.解答:
 解:作B关于CD的对称点E,则E正好在圆周上,
解:作B关于CD的对称点E,则E正好在圆周上,连接OA、OB、OE、AE,AE交CD于P,
则AP+BP最短,
∵
 的度数为60°,点B是
的度数为60°,点B是 的中点,
的中点,∴
 =
= ,且
,且 的度数是30°,
的度数是30°,∴∠AOB=∠COB=30°,
∵B关于CD的对称点是E,
∴弧BE的度数是60°,
∴∠AOE=90°,
∵OA=OE=
 CD=1,
CD=1,∴△OAE是等腰直角三角形,
由勾股定理得:AE=
 .
.故答案为:
 .
.点评:此题主要考查了轴对称最短路线,关键是找出P点位置.

练习册系列答案
相关题目
 2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )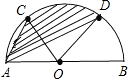 如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
 22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有
22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有 如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( )
如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( ) (2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
(2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )