题目内容
（2010•柳州）如图，从热气球P上测得两建筑物A、B的底部的俯视角分别为45°和30°，如果A、B两建筑物的距离为90m，P点在地面上的正投影恰好落在线段AB上，求热气球P的高度．（结果精确到0.01m，参考数据：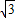
≈1.732，
≈1.414）
【答案】分析：过P作AB的垂线，设垂足为C．分别在Rt△APC和Rt△BPC中，用PC表示出AC、BC的长，进而由AB=AC+BC=90求得PC的长，即热气球P的高度．
解答：
解：过P作PC⊥AB于C点．
Rt△APC中，∠APC=45°，则AC=PC；
Rt△BPC中，∠B=30°，则BC=
PC．
∵AB=AC+BC=（
+1）PC=90，
∴PC=
≈32.94（米）．
答：热气球P的高度约为32.94米．
点评：本题考查仰角、俯角的定义，要求学生能借助仰角、俯角构造直角三角形并解直角三角形．
解答：
解：过P作PC⊥AB于C点．Rt△APC中，∠APC=45°，则AC=PC；
Rt△BPC中，∠B=30°，则BC=
PC．∵AB=AC+BC=（
+1）PC=90，∴PC=
≈32.94（米）．答：热气球P的高度约为32.94米．
点评：本题考查仰角、俯角的定义，要求学生能借助仰角、俯角构造直角三角形并解直角三角形．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
（2010•柳州）如图，AB为⊙O的直径，且弦CD⊥AB于E，过点B的切线与AD的延长线交于点F．
，DF=3，求⊙O的半径．
