题目内容
13.不等式组$\left\{\begin{array}{l}{20-x>5}\\{2(x+1)+2≤\frac{10x}{3}}\end{array}\right.$的整数解共有12个.分析 先求出不等式组的解集,再求出不等式组的整数解,即可得出答案.
解答 解:$\left\{\begin{array}{l}{20-x>5①}\\{2(x+1)+2≤\frac{10x}{3}②}\end{array}\right.$
∵解不等式①得:x<15,
解不等式②得:x≥3,
∴不等式组的解集为3≤x<15,
不等式组的整数解为3,4,5,6,7,8,9,10,11,12,13,14,共12个,
故答案为:12.
点评 本题考查了解一元一次不等式组和不等式组的整数解,能求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
3.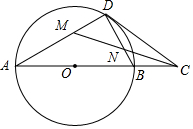 如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
(1)求证:DM=DN
(2)若AB=6,BC=2,求tan∠ACM的值.
 如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M(1)求证:DM=DN
(2)若AB=6,BC=2,求tan∠ACM的值.
4.关于x的不等式x-m>0,恰有两个负整数解,则m的取值范围是( )
| A. | -3<m<-2 | B. | -3≤m<-2 | C. | -3≤m≤-2 | D. | -3<m≤-2 |
 如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.
如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.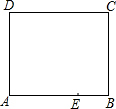 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上的一点,AE=5,点P在长方形ABCD的一边上,要使△AEP是等腰三角形,则△AEP的底边长为5或5$\sqrt{2}$或4$\sqrt{5}$.
如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上的一点,AE=5,点P在长方形ABCD的一边上,要使△AEP是等腰三角形,则△AEP的底边长为5或5$\sqrt{2}$或4$\sqrt{5}$.