题目内容
 如图所示,E、F?ABCD对角线AC上的两点,且BE∥DF.
如图所示,E、F?ABCD对角线AC上的两点,且BE∥DF.求证:
(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:(1)由平行四边形的性质可得AB=CD,∠BAE=∠DCF,结合BE∥DF,可得到∠BEA=∠DFC,可证明△ABE≌△CDF;
(2)由(1)可得到BE=DF,结合BE∥DF可证得结论.
(2)由(1)可得到BE=DF,结合BE∥DF可证得结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
∵BE∥DF,
∴∠BEF=∠DFE,
∴∠BEA=∠DFC,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS);
(2)由(1)可知△ABE≌△CDF,
∴BE=DF,
又∵BE∥DF,
∴四边形BFDE为平行四边形.
∴AB=CD,∠BAE=∠DCF,
∵BE∥DF,
∴∠BEF=∠DFE,
∴∠BEA=∠DFC,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(AAS);
(2)由(1)可知△ABE≌△CDF,
∴BE=DF,
又∵BE∥DF,
∴四边形BFDE为平行四边形.
点评:本题主要考查平行四边形的性质和判定,掌握平行四边形的性质和判定是解题的关键,即平行四边形的对边平行且相等、对角相等、对角线互相平分.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
在?ABCD中,增加下列条件中的一个,就能断定它是矩形的是( )
| A、∠A+∠C=180° |
| B、AB=BC |
| C、AC⊥BD |
| D、AC=2AB |

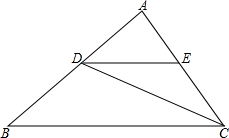 如图,点D、E分别在△ABC的边AB、AC上,AD=4,BD=5,DE∥BC,∠ACD=∠B.
如图,点D、E分别在△ABC的边AB、AC上,AD=4,BD=5,DE∥BC,∠ACD=∠B.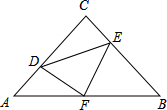 如图,在等腰Rt△ABC中,∠C=90°,AC=6,F是AB边上的中点,点D、E分别在AC、BC边上运动,连结DE、DF、EF,且保持DF⊥EF,在此运动变化的过程中,当△ADF与△BEF的面积为1:2,则DE的长为
如图,在等腰Rt△ABC中,∠C=90°,AC=6,F是AB边上的中点,点D、E分别在AC、BC边上运动,连结DE、DF、EF,且保持DF⊥EF,在此运动变化的过程中,当△ADF与△BEF的面积为1:2,则DE的长为