题目内容
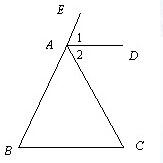
27、完成下列证明过程：如图，∠CAE是△ABC的一个外角，∠1=∠2，AD∥BC，求证：AB=AC．
证明：∵AD∥BC（已知）
∴∠1=∠
B
（两直线平行，同位角相等）∠2=∠
C
（两直线平行，内错角相等
）又∵∠1=∠2（已知）
∴
∠B
=∠C
（等量代换）∴AB=AC （
等角对等边
）．分析：根据平行线的性质和等角对等边的性质填空．
解答：证明：∵AD∥BC（已知）
∴∠1=∠B（两直线平行，同位角相等）
∠2=∠C（两直线平行，内错角相等）
又∵∠1=∠2（已知）
∴∠B=∠C（等量代换）
∴AB=AC（等角对等边）．
∴∠1=∠B（两直线平行，同位角相等）
∠2=∠C（两直线平行，内错角相等）
又∵∠1=∠2（已知）
∴∠B=∠C（等量代换）
∴AB=AC（等角对等边）．
点评：本题主要利用平行线的性质和等角对等边的性质，书写证明过程是本题练习的重点．
练习册系列答案
相关题目
22、填空，完成下列证明过程．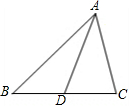
填空，完成下列证明过程．
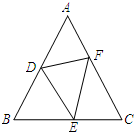填空，完成下列证明过程．
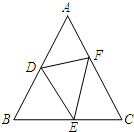填空，完成下列证明过程．