题目内容
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
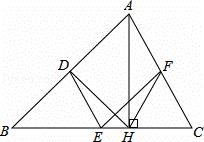
证明:(1)∵点D,E,F分别是AB,BC,CA的中点,
∴DE、EF都是△ABC的中位线,
∴EF∥AB,DE∥AC,
∴四边形ADEF是平行四边形;
(2)∵四边形ADEF是平行四边形,
∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,AH是边BC上的高,
∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,
∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,
∴∠DHF=∠DEF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
)为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 1480 | 1460 | … |
| B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的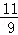 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.

 )÷
)÷ ,其中x=cos60°.
,其中x=cos60°. 的解集是
的解集是  ﹣1)0﹣
﹣1)0﹣ .
.
 ,那么sinɑ>cosɑ③一正多边形的一个外角是45°,则此图形是正八边形;④若式子
,那么sinɑ>cosɑ③一正多边形的一个外角是45°,则此图形是正八边形;④若式子 有意义,则x>1;⑤在反比例函数
有意义,则x>1;⑤在反比例函数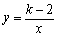 中,若x>0 时,y随x的增大而增大,则k的取值范围是k>2;其中假命题有( )
中,若x>0 时,y随x的增大而增大,则k的取值范围是k>2;其中假命题有( )