��Ŀ����
��Ϊӭ���й�ɭ���ᣬij�̼Ҽƻ��ӳ��Ҳɹ�A��B���ֲ�Ʒ��20������Ʒ�IJɹ����ۣ�Ԫ/�����Dzɹ�������������һ�κ������±��ṩ�˲��ֲɹ����ݣ�
| �ɹ����������� | 1 | 2 | �� |
| A��Ʒ���ۣ�Ԫ/���� | 1480 | 1460 | �� |
| B��Ʒ���ۣ�Ԫ/���� | 1290 | 1280 | �� |
��1����A��Ʒ�IJɹ�����Ϊx���������ɹ�����Ϊy1��Ԫ/��������y1��x�Ĺ�ϵʽ��
��2�����̼��볧��Э�̣��ɹ�A��Ʒ������������B��Ʒ������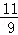 ����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ���������
����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ���������
��3�����̼ҷֱ���1760Ԫ/����1700Ԫ/�������۵����۳�A��B���ֲ�Ʒ����ȫ�����꣬�ڣ�2���������£���ɹ�A�ֲ�Ʒ���ټ�ʱ������������������
�⣺��1����y1��x�Ĺ�ϵʽy1=kx+b��
�ɱ�֪ ��
��
���k=��20��b=1500��
��y1=��20x+1500��0��x��20��x������
��2����������ɵ�
 ��
��
���11��x��15��
��x������
��x��ȡ��ֵΪ��11��12��13��14��15��
����̼ҹ���5�ֽ���������
��3����������ΪW��
��W=30x2��540x+1200��
=30��x��9��2+9570��
��a=30��0��
�൱x��9ʱ��W��x�����������
��11��x��15��
�൱x=15ʱ��W���=10650��

 ��x <n+
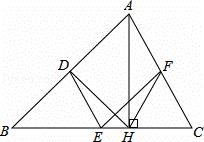
��x <n+ 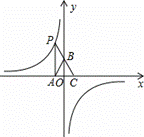 ��ͼ����P�Ƿ���������
��ͼ����P�Ƿ���������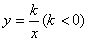 ͼ���ϵĵ㣬PA��ֱ
ͼ���ϵĵ㣬PA��ֱ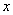 ���ڵ�A����1��0������C������Ϊ��1��0����PC��
���ڵ�A����1��0������C������Ϊ��1��0����PC��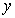 ���ڵ�B������AB����֪AB=
���ڵ�B������AB����֪AB=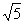
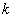 ��ֵ��__________��
��ֵ��__________�� ��
�� ���Ǹ÷���������ͼ���ϵĵ㣬������
���Ǹ÷���������ͼ���ϵĵ㣬������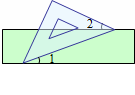
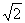 CE + PC=
CE + PC=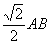 ��
��
 ��ֵ���ڣ� ��
��ֵ���ڣ� �� B.
B.  C .
C .  D .
D . 
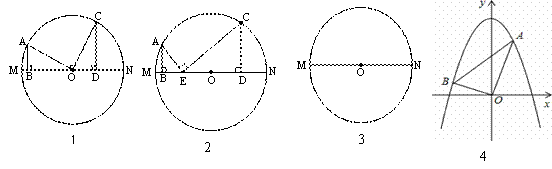 ����չǨ�ƣ���ͼ4����ƽ��ֱ������ϵ�У������߾���A��m��6����B��n��1�����㣨����0��m��3��������y��Ϊ�Գ��ᣬ�ҡ�AOB=90�㣬����mn��ֵ�����������ߵĽ���ʽ��
����չǨ�ƣ���ͼ4����ƽ��ֱ������ϵ�У������߾���A��m��6����B��n��1�����㣨����0��m��3��������y��Ϊ�Գ��ᣬ�ҡ�AOB=90�㣬����mn��ֵ�����������ߵĽ���ʽ��