题目内容
10.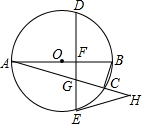 如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=$\frac{4}{3}$,则tan∠DEH=( )
如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=$\frac{4}{3}$,则tan∠DEH=( )| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
分析 连接OE,如图2,根据切线的性质得OE⊥EH,则∠OEF+∠DEH=90°,而∠OEF+∠FOE=90°,根据等角的余角相等得∠FOE=∠DEH,求出OF、EF,在Rt△OEF中,根据tan∠DEH=tan∠EOF=$\frac{EF}{OF}$ 计算即可.
解答 解:连接OE,如图2,
∵EH为⊙O的切线,
∴OE⊥EH,
∴∠OEF+∠DEH=90°,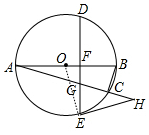
而∠OEF+∠FOE=90°,
∴∠FOE=∠DEH,
∵AF=3,FB=$\frac{4}{3}$,
∴AB=AF+BF=$\frac{13}{3}$,
∴OB=$\frac{1}{2}$AB=$\frac{13}{6}$,
∴OF=OB-FB=$\frac{5}{6}$,
在Rt△OEF中,OE=$\frac{13}{6}$,OF=$\frac{5}{6}$,
∴EF=$\sqrt{O{E}^{2}-O{F}^{2}}$=$\sqrt{(\frac{13}{6})^{2}-(\frac{5}{6})^{2}}$=2.
∴tan∠DEH=tan∠EOF=$\frac{EF}{OF}$=$\frac{2}{\frac{5}{6}}$=$\frac{12}{5}$.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理和解直角三角形.

练习册系列答案
相关题目
1.抛物线y=x2向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是( )
| A. | y=(x+8)2-9 | B. | y=(x-8)2+9 | C. | y=(x-8)2-9 | D. | y=(x+8)2+9 |
5. 如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
 如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )| A. | -$\frac{5}{2}$ | B. | -$\frac{10}{3}$ | C. | -4 | D. | -5 |
2.为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果做了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是( )
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
19.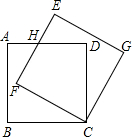 如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
 如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
如图,边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 9 | D. | 6$\sqrt{3}$ |
 如图,在等腰Rt△ABC中,∠BAC=90°.将直角边足够长的Rt△EPF的直角顶点P放在线段BC的中点上,以点P为旋转中心,转动Rt△EPF并使它的两直角边PE,PF分别与AC,AB相交于点N,M,连MN,AP,交于D点,则下列几组量:
如图,在等腰Rt△ABC中,∠BAC=90°.将直角边足够长的Rt△EPF的直角顶点P放在线段BC的中点上,以点P为旋转中心,转动Rt△EPF并使它的两直角边PE,PF分别与AC,AB相交于点N,M,连MN,AP,交于D点,则下列几组量: