题目内容
 如图所示,在三角形ABC中,∠C=90°,AB=13cm,AC=5cm,求三角形ABC的面积为多少cm2?
如图所示,在三角形ABC中,∠C=90°,AB=13cm,AC=5cm,求三角形ABC的面积为多少cm2?
解:在直角三角形中,∠C=90°,
∴AC2+BC2=AB2,
∴BC= cm=
cm=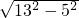 cm=12cm,
cm=12cm,
故三角形面积S= ×AC×BC=
×AC×BC= ×5cm×12cm=30cm2,
×5cm×12cm=30cm2,
答:三角形的面积为30cm2.
分析:直角三角形中,已知斜边长和以直角边长,根据勾股定理可以计算另一直角边的长度,AC2+BC2=AB2.求得BC,△ABC的面积为S= ×AC×BC.
×AC×BC.
点评:本题考查了直角三角形中勾股定理的运用,考查了直角三角形面积的计算,本题中正确的计算BC的长度是解题的关键.
∴AC2+BC2=AB2,
∴BC=
 cm=
cm=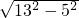 cm=12cm,
cm=12cm,故三角形面积S=
 ×AC×BC=
×AC×BC= ×5cm×12cm=30cm2,
×5cm×12cm=30cm2,答:三角形的面积为30cm2.
分析:直角三角形中,已知斜边长和以直角边长,根据勾股定理可以计算另一直角边的长度,AC2+BC2=AB2.求得BC,△ABC的面积为S=
 ×AC×BC.
×AC×BC.点评:本题考查了直角三角形中勾股定理的运用,考查了直角三角形面积的计算,本题中正确的计算BC的长度是解题的关键.

练习册系列答案
相关题目

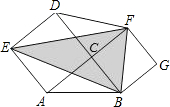 如图所示,在三角形ABC中,∠ACB=90°,AC=8厘米,BC=6厘米.分别以AC、BC为边作正方形AEDC、BCFG,则三角形BEF的面积是
如图所示,在三角形ABC中,∠ACB=90°,AC=8厘米,BC=6厘米.分别以AC、BC为边作正方形AEDC、BCFG,则三角形BEF的面积是 如图所示,在三角形ABC中,D,E分别是BC,AC上的点,AD,BE相交于F,求证:∠C+∠1+∠2+∠3=180°.
如图所示,在三角形ABC中,D,E分别是BC,AC上的点,AD,BE相交于F,求证:∠C+∠1+∠2+∠3=180°. 如图所示,在三角形ABC中,∠C=90゜,两直角边AC=6,BC=8,三角形内有-点P,它到各边的距离相等,则这个距离是( )
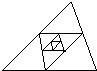
如图所示,在三角形ABC中,∠C=90゜,两直角边AC=6,BC=8,三角形内有-点P,它到各边的距离相等,则这个距离是( ) 任意一个三角形,如图所示,在三角形ABC中取各边中点依次为D、E、F,连接D、E、EF、FD得到三角形DEF,回答下列问题:
任意一个三角形,如图所示,在三角形ABC中取各边中点依次为D、E、F,连接D、E、EF、FD得到三角形DEF,回答下列问题: