Question

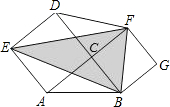如图所示，在三角形ABC中，∠ACB=90°，AC=8厘米，BC=6厘米．分别以AC、BC为边作正方形AEDC、BCFG，则三角形BEF的面积是

 

平方厘米，AEDFGB的面积是

 

平方厘米．

Answer 1

分析：△BEF可证它是等腰三角形，因而它的高为两个正方形对角线的和减去小正方形对角线的一半，底边BF为小正方形对角线的长，可求出面积；AEDFGB的面积是两个小正方形的面积加上两个直角三角形的面积．

解答：解：在△BEF中

DE=AE ∠EDF=∠ DF=AB

EAB，
∴△EDF≌△EAB，
∴EF=EB，
大正方形的对角线长为

82+82

=8

2

，小正方形对角线的长为

62+62

=6

2

，
△BEF中BF边上的高为8

2

+3

2

=11

2

，
BF=6

2

，
所以△BEF的面积为

1

2

×6

2

×11

2

=66平方厘米，
AEDFGB的面积为8²+6²+

1

2

×6×8+

1

2

×6×8=148平方厘米．
故答案为：66；148．

点评：本题考查正方形的性质，三角形的面积等知识点，关键是求△BEF的面积时，能找出底和高，求AEDFGB的面积时把这个一般多边形分成特殊的多边形或三角形来求．