题目内容
已知△ABC的三边长分别为a+1，a+2，a+3，△ABC是直角三角形时，求a的值．
考点：勾股定理
专题：
分析：直接根据勾股定理列出关于a的方程，求出a的值即可．
解答：解：∵△ABC的三边长分别为a+1，a+2，a+3，△ABC是直角三角形，
∴（a+3）2=（a+1）2+（a+2）2，
解得a=2或a=-2（舍去）．
∴a=2．
∴（a+3）2=（a+1）2+（a+2）2，
解得a=2或a=-2（舍去）．
∴a=2．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
已知a，b，c表示的数如图所示，则-a，-b，-c由小到大的顺序是（ ）| A、-a＜-b＜-c |
| B、-c＜-a＜-b |
| C、-a＜-c＜-b |
| D、-b＜-c＜-a |
，则实际纸上的号码是若三角形的两边长分别为3和5，则其周长c的取值范围是（ ）
| A、6＜c＜15 |
| B、6＜c＜16 |
| C、11＜c＜13 |
| D、10＜c＜16 |
下列计算正确的是（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
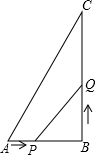在△ABC中，∠B=90°，AB=6cm，BC=12cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B沿BC向点C以2cm/s的速度移动．如果点P、Q分别从A、B同时出发．