题目内容
已知正比例函数y1=k1x,反比例函数y2=
.
(1)若y=y1+y2,当x=1时,y=-3;当x=-2时,y=3.求y与x之间的函数关系;
(2)若再同一直角坐标系中,y1和y2没有交点,试确定两个常数的乘积k1k2的取值范围.
| k2 | x |
(1)若y=y1+y2,当x=1时,y=-3;当x=-2时,y=3.求y与x之间的函数关系;
(2)若再同一直角坐标系中,y1和y2没有交点,试确定两个常数的乘积k1k2的取值范围.
分析:(1)根据题意得方程组:
,解此方程组即可求得答案;
(2)由y1和y2没有交点,可得方程k1x=
无解,即k1x2-k2=0无解,然后由判别式△<0,即可求得两个常数的乘积k1k2的取值范围.
|
(2)由y1和y2没有交点,可得方程k1x=
| k2 |
| x |
解答:解:(1)根据题意得:
,
解得:
,
故y与x之间的函数关系为:y=y1+y2=-x-
;
(2)∵y1和y2没有交点,
∴方程k1x=
无解,
即k1x2-k2=0无解,
∴△=0+4k1k2<0,
∴两个常数的乘积k1k2的取值范围为:k1k2<0.
|
解得:
|
故y与x之间的函数关系为:y=y1+y2=-x-
| 2 |
| x |
(2)∵y1和y2没有交点,
∴方程k1x=
| k2 |
| x |
即k1x2-k2=0无解,
∴△=0+4k1k2<0,
∴两个常数的乘积k1k2的取值范围为:k1k2<0.
点评:此题考查了反比例函数与一次函数的交点问题.此题难度适中,注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
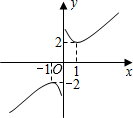 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题: 已知正比例函数y1=x,反比例函数
已知正比例函数y1=x,反比例函数