题目内容
已知正比例函数y1=k1x和反比例函数y2=| k2 | x |
分析:把A(2,-1)代入两个函数解析式即可求得两个函数解析式,两个函数解析式组成方程组就能求出交点坐标.
解答:解:将A(2,-1)代入y1=k1x中,
∴k1=-
,∴y1=-
x,
将A(2,-1)代入y2=
中,
∴k2=-2,∴y2=-
,
由
得,
∴-
x=-
,
∴x=±2(舍去x=2),
所以另一个交点为B(-2,1).
∴k1=-
| 1 |
| 2 |
| 1 |
| 2 |
将A(2,-1)代入y2=
| k2 |
| x |
∴k2=-2,∴y2=-
| 2 |
| x |
由
|
∴-
| 1 |
| 2 |
| 2 |
| x |
∴x=±2(舍去x=2),
所以另一个交点为B(-2,1).
点评:此题主要考查了:①过某个点,这个点的坐标应适合这个函数解析式;
②两个函数的交点坐标即为这两个函数解析式组成的方程组的解.
②两个函数的交点坐标即为这两个函数解析式组成的方程组的解.

练习册系列答案
相关题目
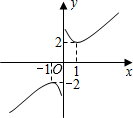 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题: 已知正比例函数y1=x,反比例函数
已知正比例函数y1=x,反比例函数