题目内容
点P是⊙O内一点，OP=2，如果⊙O的半径是3，那么过P点的最短弦长是分析：过P点作垂直于OP的弦AB，连接OA，由勾股定理可求出PA的长，进而可由垂径定理得到弦AB的长（即过P点的最短弦长）．
解答：
解：如图；过P作AB⊥OP，交⊙O于AB，连接OA；
Rt△OAP中，OP=2，OA=3，
由勾股定理，得：AP=
=
=
；
∴AB=2AP=2
；
故过P点的最短弦长是2
．
解：如图；过P作AB⊥OP，交⊙O于AB，连接OA；Rt△OAP中，OP=2，OA=3，
由勾股定理，得：AP=
| OA2-OP2 |
| 32-22 |
| 5 |
∴AB=2AP=2
| 5 |
故过P点的最短弦长是2
| 5 |
点评：此题主要考查的是垂径定理及勾股定理的应用，能够正确的判断出过P点的最短弦的位置是解答此题的关键．
练习册系列答案
相关题目
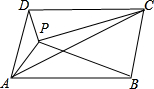如图，点P是?ABCD内一点，S△PAB=7，S△PAD=4，则S△PAC=
1、点P是△ABC内一点，连接BP并延长交AC于D，连接PC，则图中∠1，∠2，∠A的大小关系是（ ）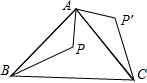
如图，△ABC是等腰直角三角形，BC是斜边，点P是△ABC内一点，△ABP绕点A逆时针旋转后与△ACP′重合，如果AP=
如图，点O是△ABC内一点，∠A=80°，∠ABO=15°，∠ACO=40°，则∠BOC等于（ ）