题目内容
阅读下列材料:
某同学在计算3×(4+1)(42+1)时,把3写成4-1后,发现可以连续运用平方差公式计算:3×(4+1)(42+1)=(4-1)(4+1)(42+1)=(42-1)(42+1)=162-1.很受启发,后来在求(2+1)(22+1)(24+1)(28+1)…(21024+1)的值时,又改造此法,将乘积式前面乘以1,且把1写为2-1得(2+1)(22+1)(24+1)(28+1)…(21024+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)…(21024+1)
=(22-1)(22+1)(24+1)(28+1)…(21024+1)
=(24-1)(24+1)(28+1)… (21024+1)=…
(21024+1)=…
=(21024-1)(21024+1)=22048-1.
回答下列问题:
(1)请借鉴该同学的经验,计算:
(3+1)(32+1)(34+1)( 38+1).
38+1).
(2)借用上面的方法,再逆用 平方差公式计算:
平方差公式计算:
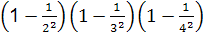 …
…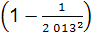 .
.
【解析】(1)(3+1)(32+1)(34+1)(38+1)
= (32-1)(32+1)(34+1)(38+1)
(32-1)(32+1)(34+1)(38+1)
= (34-1)(34+1)(38+1)=
(34-1)(34+1)(38+1)= (38-
(38- 1)(38+1)
1)(38+1)
= (316-1).
(316-1).
(2)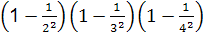 …
…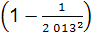
=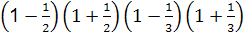 …
…
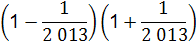
= ×
× ×
× ×
× ×…×
×…×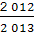 ×
×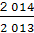
= ×
×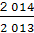 =
=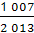 .
.

练习册系列答案
相关题目
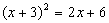
 3b件,每件打八折,则5月份该品牌衬衣的营业额比4月份增加( )
3b件,每件打八折,则5月份该品牌衬衣的营业额比4月份增加( ) 中x=4.
中x=4.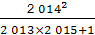 = .
= . mn+4n2的值是 .
mn+4n2的值是 . 计算正确的是( )
计算正确的是( ) B、
B、
 D
D