题目内容
4.已知点A的坐标是(-5,10),点B的坐标是(x,x-1),直线AB∥y轴,则x的值是( )| A. | -5 | B. | 11 | C. | 5 | D. | -9 |
分析 在平面直角坐标系中与y轴平行,则它上面的点横坐标相同,可求B点横坐标.
解答 解:∵AB∥y轴,
∴点B横坐标与点A横坐标相同,为-5,
可得:x=-5,
故选A
点评 此题考查平面直角坐标系中平行特点,解决本题的关键是在平面直角坐标系中与y轴平行,则它上面的点横坐标相同.

练习册系列答案
相关题目
12.将一元二次方程3x2+1=6x化为一般形式后,常数项为1,则一次项系数为( )
| A. | 3 | B. | -6 | C. | -3 | D. | 6 |
19.某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
前20天每天的价格y1(元/件)与时间t(天)的函数关系式为:y1=$\frac{1}{4}$t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=-$\frac{1}{4}$t+40(21≤t≤40且t为整数).
(1)认真分析表中的数据,用所学过的一次函数,二次函数的知识确定一个满足这些数据m(件)与t(天)之间的关系式;
(2)请计算40天中娜一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程,公司通过销售记录发现,前20天中扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
| 时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
| 日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
(1)认真分析表中的数据,用所学过的一次函数,二次函数的知识确定一个满足这些数据m(件)与t(天)之间的关系式;
(2)请计算40天中娜一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程,公司通过销售记录发现,前20天中扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
16.如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是( )
| A. | y=(x-1)2 | B. | y=(x+1)2 | C. | y=x2-1 | D. | y=x2+1 |
 已知:如图,∠EAC是△ABC的一个外角,AD平分∠EAC,AD∥BC.求证:△ABC是等腰三角形.
已知:如图,∠EAC是△ABC的一个外角,AD平分∠EAC,AD∥BC.求证:△ABC是等腰三角形.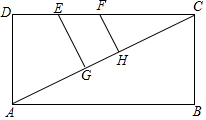 已知:如图,矩形ABCD中,E,F是CD的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=$\sqrt{5}$.
已知:如图,矩形ABCD中,E,F是CD的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=$\sqrt{5}$. 从棱长为4的正方体毛坯的一角挖去一个棱长为1的正方体,得到一个如图所示的零件,则这个零件的表面积为96.
从棱长为4的正方体毛坯的一角挖去一个棱长为1的正方体,得到一个如图所示的零件,则这个零件的表面积为96. 一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于120°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是60°.
一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于120°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是60°.