Question

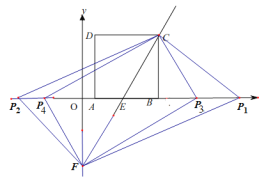
【题目】如图，将边长为3的正方形置于平面直角坐标系第一象限，使边落在轴的正半轴上，直线：经过点且与轴交于点．

（1）求点坐标；

（2）求的面积；

（3）若直线与轴交于点，在轴上是否存在点，使得是直角三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）；（3）存在，，，，.

【解析】

（1）由正方形的性质可知点C的纵坐标为3，把y=3代入即可求出点C的坐标；

（2）先求出点E的坐标，再根据三角形的面积公式求解即可；

（3）分四种情况求解即可：①当FCP1=90°时，②当CFP2=90°时，③当CP3F=90°时，④当CP4F=90°时．

（1）∵正方形的边长为3，

∴AD=AB=3，

当y=3时，，

∴x=4，

∴；

（2）把代入得，∴，

又∵，∴，

∴；

（3）当x=3时，，

∴，

∵，，

∴CE=，CF=，

∴EF=CE=．

①当FCP1=90°时，设P1(x，0)，

∵CP12=BC2+BP12=EP1-CE2，

∴9+(x-4)2=(x-2)2-13，

解得

x=，

∴;

②当CFP2=90°时，

与①同理可求；

③当CP3F=90°时，

∵EF=CE=，

∴EP3=EF=CE=，

∴OP3=2+，

∴;

④当CP4F=90°时，

与③同理可求．

综上可知，，，，．