题目内容
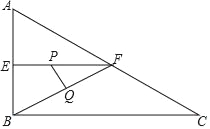
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2cm,E、F分别是AB、AC的中点,动点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时动点Q从点B出发,沿BF方向匀速运动,速度为2cm/s,连接PQ,设运动时间为ts(0<t<1),则当t=___时,△PQF为等腰三角形.
【答案】2﹣![]() 或
或![]() .
.
【解析】
由勾股定理和含30°角的直角三角形的性质先分别求出AC和BC,然后根据题意把PF和FQ表示出来,当△PQF为等腰三角形时分三种情况讨论即可.
解:∵∠ABC=90°,∠ACB=30°,AB=2cm,
∴AC=2AB=4cm,BC=![]() =2
=2![]() ,
,
∵E、F分别是AB、AC的中点,
∴EF=![]() BC=
BC=![]() cm,BF=
cm,BF=![]() AC=2cm,
AC=2cm,
由题意得:EP=t,BQ=2t,
∴PF=![]() ﹣t,FQ=2﹣2t,
﹣t,FQ=2﹣2t,
分三种情况:
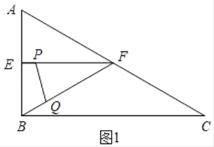
①当PF=FQ时,如图1,△PQF为等腰三角形.
则![]() ﹣t=2﹣2t,
﹣t=2﹣2t,
t=2﹣![]() ;
;
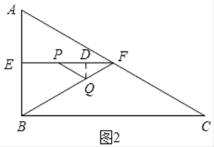
②如图2,当PQ=FQ时,△PQF为等腰三角形,过Q作QD⊥EF于D,
∴PF=2DF,
∵BF=CF,
∴∠FBC=∠C=30°,
∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠PFQ=∠FBC=30°,
∵FQ=2﹣2t,
∴DQ=![]() FQ=1﹣t,
FQ=1﹣t,
∴DF= ![]() (1﹣t),
(1﹣t),
∴PF=2DF=2![]() (1﹣t),
(1﹣t),
∵EF=EP+PF= ![]() ,
,
∴t+2![]() (1﹣t)=
(1﹣t)=![]() ,
,
t= ![]() ;
;
③因为当PF=PQ时,∠PFQ=∠PQF=30°,
∴∠FPQ=120°,
而在P、Q运动过程中,∠FPQ最大为90°,所以此种情况不成立;
综上,当t=2﹣![]() 或
或![]() 时,△PQF为等腰三角形.
时,△PQF为等腰三角形.
故答案为:2﹣![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目