题目内容
19.下列条件中,能够证明两个三角形全等的有( )①两边及其中一边上的中线对应相等; ②两角及第三个角的角平分线对应相等;
③两个直角三角形任意两条对应边相等;④两个等腰三角形任意两条对应边相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据三角形全等的判定方法可判断①②③正确,当两个等腰三角形两腰对应相等时,这两个三角形不一定全等,则可对④进行判断.
解答 解:两边及其中一边上的中线对应相等的两个三角形全等,所以①正确;
两角及第三个角的角平分线对应相等的两个三角形全等,所以②正确;
两个直角三角形任意两条对应边相等,则两个直角三角形全等,所以③正确;
两个等腰三角形任意两条对应边相等,这两个三角形不一定全等,所以④错误.
故选C.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.某商店以32元的价格购进30个茶杯,针对不同的顾客,30个茶杯的售价不完全相同,若以47元为标准,将超过的钱数记为正,不足的钱数记为负,记录结果如下表所示:
该超市售完这30个茶杯后,赚了多少钱?
| 售出个数 | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价(元) | +3 | +2 | +1 | 0 | -1 | -2 |
4.下列说法正确的是( )
| A. | 有理数是指整数、分数、正数、负数和0 | |
| B. | 0是整数,但不是自然数 | |
| C. | 在有理数中,不是正数就是负数 | |
| D. | 一个有理数不是整数就是分数 |
11.方程(x-1)2=x-1的根是( )
| A. | 1 | B. | -1 | C. | 2 | D. | 1或2 |
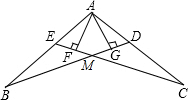 如图,AB=AC,点D、E分别在AC、AB上,AG⊥BD于点G,AF⊥CE于点F,且AE=AD,EF=DG.求证:BG=CF.
如图,AB=AC,点D、E分别在AC、AB上,AG⊥BD于点G,AF⊥CE于点F,且AE=AD,EF=DG.求证:BG=CF.