题目内容
已知△ABC中,AC=4,BC=5,AB=6.(1)如图,点D为边AC上任意一点,点E在边AB上,且△ADE与△ABC相似.
①请在图中画出所有符合题意的△ADE(不必尺规作图);
②若AD=m,试用m的代数式表示AE的长;
(2)点M、N分别在边AB、BC上,且△BMN与△ABC相似,若AM=x,试求当符合题
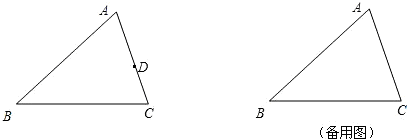 意的△BMN唯一时,x的取值范围(请写出必要的解题过程).
意的△BMN唯一时,x的取值范围(请写出必要的解题过程).
分析:(1)①过点D作BC的平行线,∠AED=∠ABC,做∠AED=∠ACB,这两种情况.
②利用相似三角形对应边成比例,将AD=m代入即可.
(2)当MN∥AC时,△BMN与△ABC相似总是存立,只要求出点N与点C重合,且△BMN∽△BCA时AM的长即可,当△BMN∽△BCA(N与C重合)时,有∠BMC=∠ACB,当符合题意的△BMN唯一时,x的取值范围是0≤x<
.
②利用相似三角形对应边成比例,将AD=m代入即可.
(2)当MN∥AC时,△BMN与△ABC相似总是存立,只要求出点N与点C重合,且△BMN∽△BCA时AM的长即可,当△BMN∽△BCA(N与C重合)时,有∠BMC=∠ACB,当符合题意的△BMN唯一时,x的取值范围是0≤x<
| 11 |
| 6 |
解答:解:(1)①如图所示
 ,
,
②情况一:∵△AED∽△ABC,且∠AED=∠ABC,
∴
=
,
∴AE=
m;(1分)
情况二:∵△ADE∽△ABC,且∠AED=∠ACB,
∴
=
,
∴AE=
m;(1分)
(2)∵当MN∥AC时,△BMN与△ABC相似总是存立,
∴只要求出点N与点C重合,且△BMN∽△BCA时AM的长即可.(1分)
当△BMN∽△BCA(N与C重合)时,有∠BMN=∠ACB,则
=
,
即
=
,
∴x=
(1分)
∴当符合题意的△BMN唯一时,x的取值范围是0≤x<
.(2分)
 ,
,②情况一:∵△AED∽△ABC,且∠AED=∠ABC,
∴
| AE |
| AB |
| AD |
| AC |
∴AE=
| 3 |
| 2 |
情况二:∵△ADE∽△ABC,且∠AED=∠ACB,
∴
| AE |
| AC |
| AD |
| AB |
∴AE=
| 2 |
| 3 |
(2)∵当MN∥AC时,△BMN与△ABC相似总是存立,
∴只要求出点N与点C重合,且△BMN∽△BCA时AM的长即可.(1分)
当△BMN∽△BCA(N与C重合)时,有∠BMN=∠ACB,则
| BC |
| BM |
| BA |
| BC |
即
| 5 |
| 6-x |
| 6 |
| 5 |
∴x=
| 11 |
| 6 |
∴当符合题意的△BMN唯一时,x的取值范围是0≤x<
| 11 |
| 6 |
点评:本题关键是要懂得利用对应角相等判定相似三角形,然后利用相似三角形的对应边成比例的性质来求解的.尤其是第(1)比较容易,(2)稍微有点难度.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( )
12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( ) 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: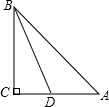 如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD.
如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD. 已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.
已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.