题目内容
（1）若cosα=
，α为锐角，则sinα=
；
（2）若tanα=2，则
=
．
| 1 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
（2）若tanα=2，则
| cos2a |
| sin2a |
| 1 |
| 4 |
| 1 |
| 4 |
分析：（1）根据sin2α+cos2α=1，可求出cosα的值．
（2）化简可得
=
，代入即可得出答案．
（2）化简可得
| cos2a |
| sin2a |
| 1 |
| tan2α |
解答：解：（1）∵sin2α+cos2α=1，cosα=
，
∴sin2α=
，
又∵α为锐角，
∴sinα=
．
（2）
=(
)2=（
）2=
．
故答案为：
、
．
| 1 |
| 3 |
∴sin2α=
| 8 |
| 9 |
又∵α为锐角，
∴sinα=
2
| ||
| 3 |
（2）
| cos2a |
| sin2a |
| cosα |
| sinα |
| 1 |
| tanα |
| 1 |
| 4 |
故答案为：
2
| ||
| 3 |
| 1 |
| 4 |
点评：本题考查了同角三角函数的关系，注意掌握据sin2α+cos2α=1，tanα=
．
| sinα |
| cosα |
练习册系列答案
备战中考寒假系列答案
相关题目
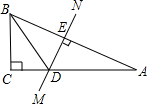如图，在△ABC中，∠C=90°，AC=9cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC=若cos（36°-A）=
，则sin（54°+A）的值是（ ）
| 7 |
| 8 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
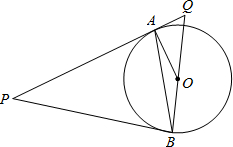=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．