题目内容
13.有一列数a1,a2,a3,…,an,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a1=2,a2=0.5 则a 2007为-1.分析 根据题意可以求出这列数的前几项,从而可以发现规律,得到题目中所求项的值.
解答 解:由题意可得,
a1=2,a2=0.5,a3=-1,a4=2,a5=0.5,a,6=-1,
∴2007÷3=669,
∴a2007=-1,
故答案为:-1.
点评 本题考查数字的变化类,解题的关键是明确题意,找出数字的变化规律.

练习册系列答案
相关题目
3.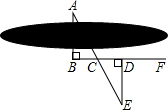 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图),判定△EDC≌△ABC的理由是( )
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图),判定△EDC≌△ABC的理由是( )
 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图),判定△EDC≌△ABC的理由是( )
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图),判定△EDC≌△ABC的理由是( )| A. | SAS | B. | ASA | C. | SSS | D. | HL |
4.六张纸牌上分别写着A、a、B、b、C、c,闭眼摸出两张,正好是同一个字母的大写与小写形式的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{5}$ |
2.若M+20=|M|+20,则M一定是( )
| A. | 任意一个有理数 | B. | 任意一个非负数 | C. | 任意一个实数 | D. | 任意一个负数 |