题目内容
10.解不等式组:(1)$\left\{\begin{array}{l}{-2x<6}\\{3(x+1)<2x+5}\end{array}\right.$并将解集在数轴上表示出来.

(2)$\left\{\begin{array}{l}{x+1≤0}\\{x≤\frac{x-2}{3}+2}\end{array}\right.$.
分析 (1)分别求出各不等式的解集,再求出其公共解集并在数轴上表示出来即可.
(2)先解不等式组中的每一个不等式,再把求出它们的公共解即可.
解答 解:(1)$\left\{\begin{array}{l}{-2x<6①}\\{3(x+1)<2x+5②}\end{array}\right.$,
由①得,x>-3,
由②得,x<2,
故此不等式组的解集为:-3<x<2.
在数轴上表示为: ;
;
(2)$\left\{\begin{array}{l}{x+1≤0①}\\{x≤\frac{x-2}{3}+2②}\end{array}\right.$
解不等式①,得 x≤-1.
解不等式②,得x≤2.
故不等式组的解集为:x≤-1.
点评 本题考查的是解一元一次不等式组,熟知“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则是解答此题的关键.

练习册系列答案
相关题目
15. 如图,在?ABCD中,∠A-∠B=40°,∠B的度数是( )
如图,在?ABCD中,∠A-∠B=40°,∠B的度数是( )
 如图,在?ABCD中,∠A-∠B=40°,∠B的度数是( )
如图,在?ABCD中,∠A-∠B=40°,∠B的度数是( )| A. | 110° | B. | 90° | C. | 70° | D. | 50° |
 (1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;
(1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$; 如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).
如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).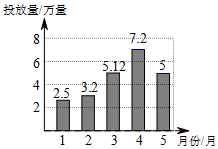 绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.已知某地区从2017年1月到5月的共享单车投放量如图所示.
绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.已知某地区从2017年1月到5月的共享单车投放量如图所示. 如图所示,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(-2,0),根据要求回答下列问题:
如图所示,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(-2,0),根据要求回答下列问题: 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.
 合并的二次根式是( )
合并的二次根式是( ) B.
B.  C.
C.  D.
D. 