题目内容
 如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2,
如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2, .
.
求梯形ABCD的面积.
解:∵AB∥CD,BC⊥AB,
∴BC⊥CD.(1分)
∵AD⊥BD,
∴∠ABD+∠A=90°.
又∵∠CBD+∠ABD=90°,
∴∠CBD=∠A.(1分)
∵ ,
,
∴ .(2分)
.(2分)
∵CD=2,
∴BD=3, .(2分)
.(2分)
又∵ ,
,
∴ .(2分)
.(2分)
∴ .(2分)
.(2分)
分析:由AD=AB,∠A=90°可得BD的长,又AD∥BC,可得△BCD为等腰直角三角形,进而可求解面积.
点评:本题考查了梯形的性质及解直角三角形的知识,掌握直角梯形的性质,会在直角梯形中求解一些简单的计算问题.
∴BC⊥CD.(1分)
∵AD⊥BD,
∴∠ABD+∠A=90°.
又∵∠CBD+∠ABD=90°,
∴∠CBD=∠A.(1分)
∵
 ,
,∴
 .(2分)
.(2分)∵CD=2,
∴BD=3,
 .(2分)
.(2分)又∵
 ,
,∴
 .(2分)
.(2分)∴
 .(2分)
.(2分)分析:由AD=AB,∠A=90°可得BD的长,又AD∥BC,可得△BCD为等腰直角三角形,进而可求解面积.
点评:本题考查了梯形的性质及解直角三角形的知识,掌握直角梯形的性质,会在直角梯形中求解一些简单的计算问题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
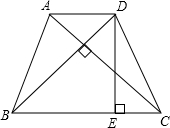 如图,已知在梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则该梯形的高DE等于
如图,已知在梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则该梯形的高DE等于 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. 27、如图,已知在梯形ABCD中,AD∥BC,AD+BC=CD,M是AB的中点,DM,CM是否分别是∠ADC和∠DCB的平分线?说明理由.
27、如图,已知在梯形ABCD中,AD∥BC,AD+BC=CD,M是AB的中点,DM,CM是否分别是∠ADC和∠DCB的平分线?说明理由.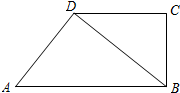 如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2,
如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2, 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.