题目内容
 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.(1)求证:四边形EFOG的周长等于2 OB;
(2)请你将上述题目的条件“梯形ABCD中,AD∥BC,AB=DC”改为另一种四边形,其他条件不变,使得结论“四边形EFOG的周长等于2 OB”仍成立,并将改编后的题目画出图形,写出已知、求证、不必证明.
分析:(1)很显然四边形OFEG是个平行四边形,那么OF=GE,OG=EF,我们可通过全等三角形ABC和DBC全等得出∠ACB=∠DBC,然后根据GE∥AC,可得出三角形BGE是等腰三角形,那么GE=GB,因此OB=OG+GE而OG=EF,GE=OF,由此可得出四边形EFOG的周长是2OB.
(2)由(1)的解题思路我们可看出,要得到(1)的结论,必须满足的条件应该是三角形ABC和DBC全等,那么AB和CD边必须相等,四边形的对角线必须相等,因此我们可将等腰梯形换成正方形或矩形,就能得出和(1)一样的结论了.
(2)由(1)的解题思路我们可看出,要得到(1)的结论,必须满足的条件应该是三角形ABC和DBC全等,那么AB和CD边必须相等,四边形的对角线必须相等,因此我们可将等腰梯形换成正方形或矩形,就能得出和(1)一样的结论了.
解答: 证明:(1)如图1
证明:(1)如图1
∵四边形ABCD是梯形,AD∥BC,AB=CD,
∴∠ABC=∠DCB.
又∵BC=CB,AB=DC,
∴△ABC≌△DCB.
∴∠1=∠2.
又∵GE∥AC,
∴∠2=∠3.
∴∠1=∠3.
∴EG=BG.
∵EG∥OC,EF∥OB,
∴四边形EGOF是平行四边形.
∴EG=OF,EF=OG.
∴四边形EGOF的周长=2(OG+GE)=2(OG+GB)=2OB
(2)方法1,如图2,已知矩形ABCD中,对角线AC、BD相交于点O,E为BC上一个动点,(点E不与B、C两点重合)EF∥BD,交AC于点F,EG∥AC交BD于点G
求证:四边形EFOG的周长等于2OB.
方法2:如图3,已知正方形ABCD中,对角线AC、BD相交于点O,E为BC上一个动点,(点E不与B、C两点重合)EF∥BD,交AC于点F,EG∥AC交BD于点G
求证:四边形EFOG的周长等于2OB.
 证明:(1)如图1
证明:(1)如图1∵四边形ABCD是梯形,AD∥BC,AB=CD,
∴∠ABC=∠DCB.
又∵BC=CB,AB=DC,
∴△ABC≌△DCB.
∴∠1=∠2.
又∵GE∥AC,
∴∠2=∠3.
∴∠1=∠3.
∴EG=BG.
∵EG∥OC,EF∥OB,
∴四边形EGOF是平行四边形.
∴EG=OF,EF=OG.
∴四边形EGOF的周长=2(OG+GE)=2(OG+GB)=2OB
(2)方法1,如图2,已知矩形ABCD中,对角线AC、BD相交于点O,E为BC上一个动点,(点E不与B、C两点重合)EF∥BD,交AC于点F,EG∥AC交BD于点G
求证:四边形EFOG的周长等于2OB.
方法2:如图3,已知正方形ABCD中,对角线AC、BD相交于点O,E为BC上一个动点,(点E不与B、C两点重合)EF∥BD,交AC于点F,EG∥AC交BD于点G
求证:四边形EFOG的周长等于2OB.
点评:本题主要考查了等腰梯形的性质,平行四边形的性质以及全等三角形的判定和应用等知识点,根据全等三角形来得出角相等是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
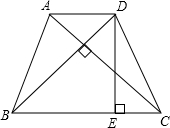 如图,已知在梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则该梯形的高DE等于
如图,已知在梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则该梯形的高DE等于 27、如图,已知在梯形ABCD中,AD∥BC,AD+BC=CD,M是AB的中点,DM,CM是否分别是∠ADC和∠DCB的平分线?说明理由.
27、如图,已知在梯形ABCD中,AD∥BC,AD+BC=CD,M是AB的中点,DM,CM是否分别是∠ADC和∠DCB的平分线?说明理由.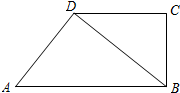 如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2,
如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2, 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.